二、填空题:把答案填在答题卡相应题号后的横线上(本大题共5小题,每小题5分,共25分)
11.设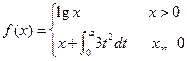 ,若
,若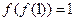 ,则
,则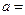 .
.
【分析】分段函数问题通常需要分布进行计算或判断,从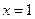 算起是解答本题的突破口.
算起是解答本题的突破口.
【解】因为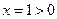 ,所以
,所以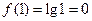 ,又因为
,又因为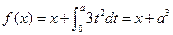 ,
,
所以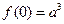 ,所以
,所以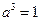 ,
,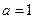 .
.
【答案】1
12.设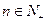 ,一元二次方程
,一元二次方程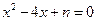 有整数根的充要条件是
有整数根的充要条件是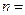 .
.
【分析】直接利用求根公式进行计算,然后用完全平方数、整除等进行判断计算.
【解】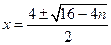
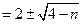 ,因为
,因为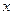 是整数,即
是整数,即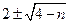 为整数,所以
为整数,所以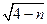 为整数,且
为整数,且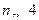 ,又因为
,又因为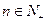 ,取
,取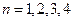 ,验证可知
,验证可知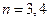 符合题意;反之
符合题意;反之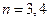 时,可推出一元二次方程
时,可推出一元二次方程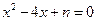 有整数根.
有整数根.
【答案】3或4
13.观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
……
照此规律,第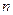 个等式为 .
个等式为 .
【分析】归纳总结时,看等号左边是子的变化规律,右边结果的特点,然后归纳出一般结论.行数、项数及其变化规律是解答本题的关键.
【解】把已知等式与行数对应起来,则每一个等式的左边的式子的第一个数是行数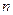 ,加数的个数是
,加数的个数是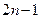 ;等式右边都是完全平方数,
;等式右边都是完全平方数,
行数 等号左边的项数
1=1 1 1
2+3+4=9 2 3
3+4+5+6+7=25 3 5
4+5+6+7+8+9+10=49 4 7
…… …… ……
所以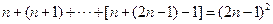 ,
,
即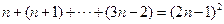
【答案】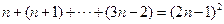
14.植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边,使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为 (米).
【分析】把实际问题转化为数学模型,然后列式转化为函数的最值问题.
【解】(方法一)设树苗放在第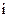 个树坑旁边(如图),
个树坑旁边(如图),

1 2 …  … 19 20
… 19 20
那么各个树坑到第i个树坑距离的和是
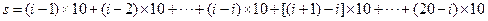
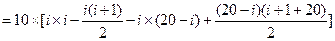
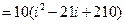 ,所以当
,所以当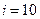 或
或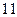 时,
时,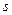 的值最小,最小值是1000,所以往返路程的最小值是2000米.
的值最小,最小值是1000,所以往返路程的最小值是2000米.
(方法二)根据图形的对称性,树苗放在两端的树坑旁边,所得路程总和相同,取得一个最值;所以从两端的树坑向中间移动时,所得路程总和的变化相同,最后移到第10个和第11个树坑旁时,所得的路程总和达到另一个最值,所以计算两个路程和即可。树苗放在第一个树坑旁,则有路程总和是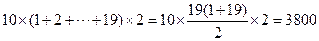 ;树苗放在第10个(或第11个)树坑旁边时,路程总和是
;树苗放在第10个(或第11个)树坑旁边时,路程总和是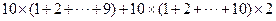
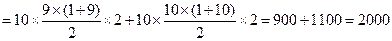 ,所以路程总和最小为2000米.
,所以路程总和最小为2000米.
【答案】2000
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
A.(不等式选做题)若关于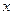 的不等式
的不等式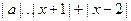 存在实数解,则实数
存在实数解,则实数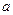 的取值范围是 .
的取值范围是 .
【分析】先确定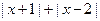 的取值范围,再使得
的取值范围,再使得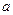 能取到此范围内的值即可.
能取到此范围内的值即可.
【解】当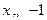 时,
时,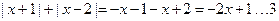 ;
;
当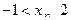 时,
时,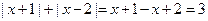 ;
;
当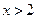 时,
时,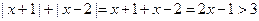 ;
;
综上可得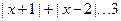 ,所以只要
,所以只要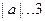 ,解得
,解得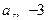 或
或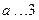 ,
,
即实数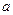 的取值范围是
的取值范围是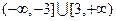 .
.
【答案】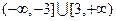
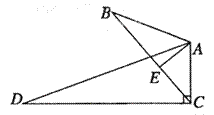
B.(几何证明选做题)如图,∠B=∠D,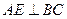 ,
,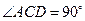 ,且AB=6,AC=4,AD=12,则BE= .
,且AB=6,AC=4,AD=12,则BE= .
【分析】寻找两个三角形相似的条件,再根据相似三角形的对应边成比例求解.
【解】因为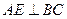 ,
,
所以∠AEB=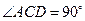 ,又因为∠B=∠D,所以△AEB∽△ACD,所以
,又因为∠B=∠D,所以△AEB∽△ACD,所以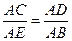 ,
,
所以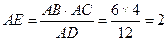 ,在Rt△AEB中,
,在Rt△AEB中,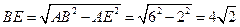 .
.
【答案】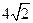
C.(坐标系与参数方程选做题)直角坐标系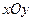 中,以原点O为极点,
中,以原点O为极点,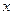 轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线
轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线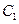 :
: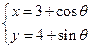 (
(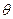 为参数)和曲线
为参数)和曲线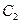 :
: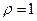 上,则
上,则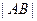 的最小值为 .
的最小值为 .
【分析】利用化归思想和数形结合法,把两条曲线转化为直角坐标系下的方程.
【解】曲线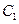 的方程是
的方程是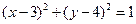 ,曲线
,曲线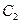 的方程是
的方程是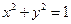 ,两圆外离,所以
,两圆外离,所以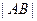 的最小值为
的最小值为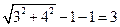 .
.
【答案】3
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6小题,共75分)
16.(本小题满分12分)
如图,在△ABC中,∠ABC=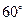 ,∠BAC
,∠BAC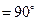 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC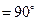 .
.
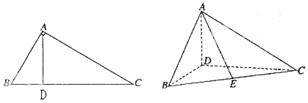
(1)证明:平面ADB⊥平面BDC;
(2)设E为BC的中点,求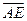 与
与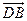 夹角的余弦值.
夹角的余弦值.
【分析】(1)确定图形在折起前后的不变性质,如角的大小不变,线段长度不变,线线关系不变,再由面面垂直的判定定理进行推理证明;(2)在(1)的基础上确定出三线两两垂直,建立空间直角坐标系,利用向量的坐标和向量的数量积运算求解.
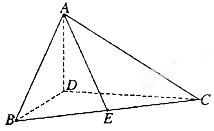
【解】(1)∵折起前AD是BC边上的高,
∴当△ABD折起后, AD⊥DC,AD⊥DB,
又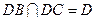 ,∴AD⊥平面BDC,
,∴AD⊥平面BDC,
∵AD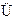 平面ABD,∴平面ABD⊥平面BDC.
平面ABD,∴平面ABD⊥平面BDC.
(2)由∠BDC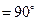 及(1)知DA,DB,DC两两垂直,不妨设|DB|=1,以D为坐标原点,以
及(1)知DA,DB,DC两两垂直,不妨设|DB|=1,以D为坐标原点,以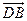 ,
,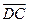 ,
,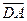 所在直线为
所在直线为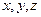 轴建立如图所示的空间直角坐标系,易得:
轴建立如图所示的空间直角坐标系,易得:
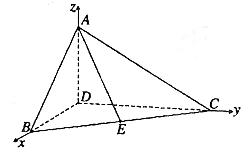
D(0,0,0),B(1,0,0),C(0,3,0),A(0,0,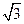 ),E(
),E(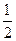 ,
,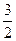 ,0),
,0),
所以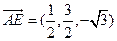 ,
,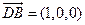 ,
,
∴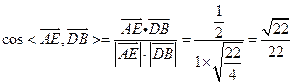
所以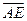 与
与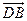 夹角的余弦值是
夹角的余弦值是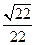 .
.












