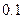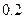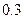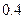17.(本小题满分12分)
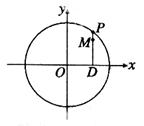
如图,设P是圆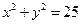 上的动点,点D是P在
上的动点,点D是P在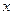 轴上投影,M为PD上一点,且
轴上投影,M为PD上一点,且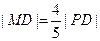 .
.
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为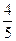 的直线被C所截线段的长度.
的直线被C所截线段的长度.
【分析】(1)动点M通过点P与已知圆相联系,所以把点P的坐标用点M的坐标表示,然后代入已知圆的方程即可;(2)直线方程和椭圆方程组成方程组,可以求解,也可以利用根与系数关系;结合两点的距离公式计算.
【解】(1)设点M的坐标是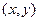 ,P的坐标是
,P的坐标是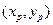 ,
,
因为点D是P在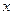 轴上投影,
轴上投影,
M为PD上一点,且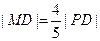 ,所以
,所以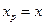 ,且
,且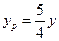 ,
,
∵P在圆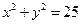 上,∴
上,∴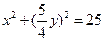 ,整理得
,整理得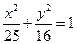 ,
,
即C的方程是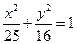 .
.
(2)过点(3,0)且斜率为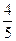 的直线方程是
的直线方程是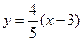 ,
,
设此直线与C的交点为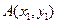 ,
,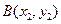 ,
,
将直线方程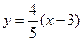 代入C的方程
代入C的方程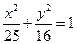 得:
得:
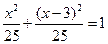 ,化简得
,化简得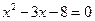 ,∴
,∴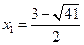 ,
,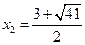 ,
,
所以线段AB的长度是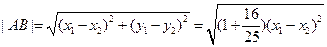
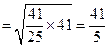 ,即所截线段的长度是
,即所截线段的长度是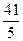 .
.
18.(本小题满分12分)
叙述并证明余弦定理.
【分析思路点拨】本题是课本公式、定理、性质的推导,这是高考考查的常规方向和考点,引导考生回归课本,重视基础知识学习和巩固.
【解】叙述:
余弦定理:三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余弦之积的两倍。或:在△ABC中,a,b,c为A,B,C的对边,有
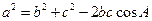 ,
,
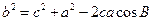 ,
,
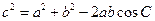 .
.
证明:(证法一) 如图,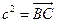
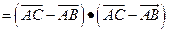
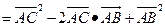
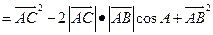
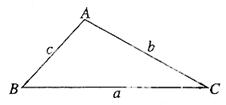
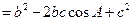
即 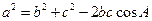
同理可证 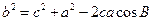 ,
,
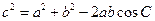
(证法二)已知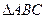 中,
中,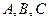 所对边分别为
所对边分别为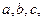 ,以
,以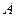 为原点,
为原点,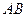 所在直线为
所在直线为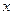 轴建立直角坐标系,则
轴建立直角坐标系,则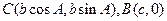 ,
,
∴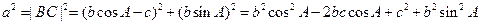
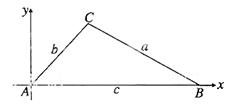
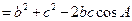 ,
,
即 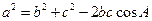
同理可证 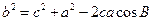 ,
,
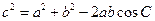
19.(本小题满分12分)
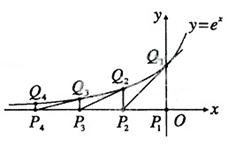
如图,从点P1(0,0)作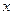 轴的垂线交曲线
轴的垂线交曲线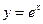 于点
于点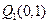 ,曲线在
,曲线在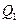 点处的切线与
点处的切线与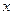 轴交于点
轴交于点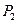 .再从
.再从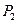 做
做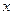 轴的垂线交曲线于点
轴的垂线交曲线于点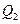 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: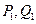 ;
;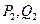 ;…;
;…;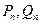 ,记
,记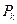 点的坐标为
点的坐标为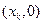 (
(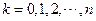 ).
).
(1)试求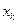 与
与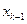 的关系(
的关系(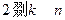 );
);
(2)求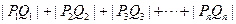 .
.
【分析】(1)根据函数的导数求切线方程,然后再求切线与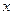 轴的交点坐标;(2)尝试求出通项
轴的交点坐标;(2)尝试求出通项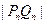 的表达式,然后再求和.
的表达式,然后再求和.
【解】(1)设点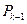 的坐标是
的坐标是 ,∵
,∵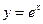 ,∴
,∴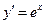 ,
,
∴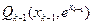 ,在点
,在点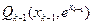 处的切线方程是
处的切线方程是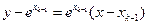 ,
,
令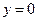 ,则
,则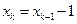 (
(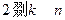 ).
).
(2)∵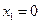 ,
,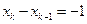 ,∴
,∴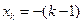 ,
,
∴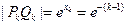 ,于是有
,于是有
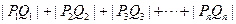
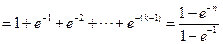
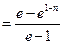 ,
,
即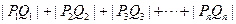
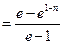 .
.
20.(本小题满分13分)
如图,A地到火车站共有两条路径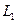 和
和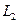 ,据统计,通过两条路径所用的时间互不影响,所用时间落在个时间段内的频率如下表:
,据统计,通过两条路径所用的时间互不影响,所用时间落在个时间段内的频率如下表:
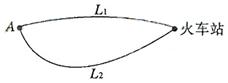
时间(分钟) | 10 | 20 | 30 | 40 | 50 |
|
|
|
|
|
|
| 0 |
|
|
|
|
现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站.
(1)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(2)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(1)的选择方案,求X的分布列和数学期望 .
【分析】(1)会用频率估计概率,然后把问题转化为互斥事件的概率;(2)首先确定X的取值,然后确定有关概率,注意运用对立事件、相互独立事件的概率公式进行计算,列出分布列后即可计算数学期望.
【解】(1)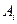 表示事件“甲选择路径
表示事件“甲选择路径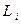 时,40分钟内赶到火车站”,
时,40分钟内赶到火车站”, 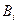 表示事件“甲选择路径
表示事件“甲选择路径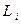 时,50分钟内赶到火车站”,
时,50分钟内赶到火车站”,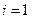 ,
,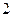 .
.
用频率估计相应的概率,则有:
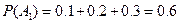 ,
,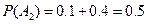 ;
;
∵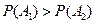 ,∴甲应选择路径
,∴甲应选择路径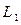 ;
;
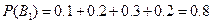 ,
,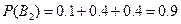 ;
;
∵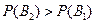 ,∴乙应选择路径
,∴乙应选择路径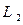 .
.
(2)用A,B分别表示针对(1)的选择方案,甲、乙在各自允许的时间内赶到火车站,由(1)知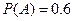 ,
,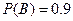 ,又事件A,B相互独立,
,又事件A,B相互独立,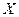 的取值是0,1,2,
的取值是0,1,2,
∴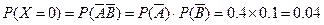 ,
,
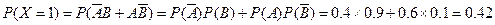
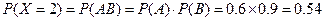 ,
,
∴X的分布列为
| 0 | 1 | 2 |
P | 0.04 | 0.42 | 0.54 |
∴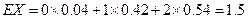 .
.
21.(本小题满分14分)
设函数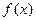 定义在
定义在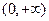 上,
上,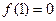 ,导函数
,导函数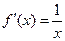 ,
,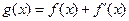 .
.
(1)求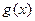 的单调区间和最小值;
的单调区间和最小值;
(2)讨论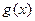 与
与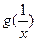 的大小关系;
的大小关系;
(3)是否存在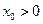 ,使得
,使得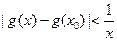 对任意
对任意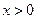 成立?若存在,求出
成立?若存在,求出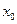 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【分析】(1)先求出原函数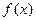 ,再求得
,再求得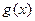 ,然后利用导数判断函数的单调性(单调区间),并求出最小值;(2)作差法比较,构造一个新的函数,利用导数判断函数的单调性,并由单调性判断函数的正负;(3)存在性问题通常采用假设存在,然后进行求解;注意利用前两问的结论.
,然后利用导数判断函数的单调性(单调区间),并求出最小值;(2)作差法比较,构造一个新的函数,利用导数判断函数的单调性,并由单调性判断函数的正负;(3)存在性问题通常采用假设存在,然后进行求解;注意利用前两问的结论.
【解】(1)∵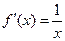 ,∴
,∴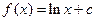 (
(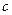 为常数),又∵
为常数),又∵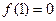 ,所以
,所以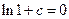 ,即
,即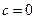 ,
,
∴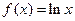 ;
;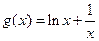 ,
,
∴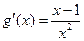 ,令
,令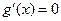 ,即
,即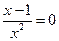 ,解得
,解得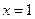 ,
,
当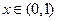 时,
时,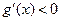 ,
,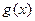 是减函数,故区间在
是减函数,故区间在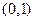 是函数
是函数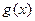 的减区间;
的减区间;
当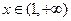 时,
时,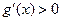 ,
,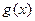 是增函数,故区间在
是增函数,故区间在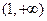 是函数
是函数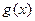 的增区间;
的增区间;
所以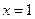 是
是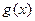 的唯一极值点,且为极小值点,从而是最小值点,
的唯一极值点,且为极小值点,从而是最小值点,
所以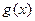 的最小值是
的最小值是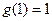 .
.
(2)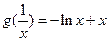 ,设
,设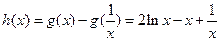 ,
,
则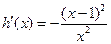 ,
,
当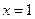 时,
时,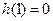 ,即
,即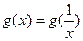 ,
,
当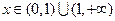 时,
时,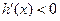 ,
,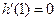 ,
,
因此函数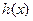 在
在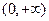 内单调递减,
内单调递减,
当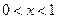 时,
时,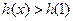 =0,∴
=0,∴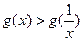 ;
;
当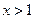 时,
时,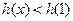 =0,∴
=0,∴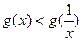 .
.
(3)满足条件的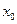 不存在.证明如下:
不存在.证明如下:
证法一 假设存在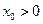 ,使
,使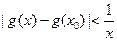 对任意
对任意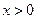 成立,
成立,
即对任意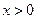 有
有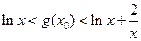 ①
①
但对上述的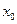 ,取
,取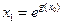 时,有
时,有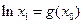 ,这与①左边的不等式矛盾,
,这与①左边的不等式矛盾,
因此不存在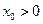 ,使
,使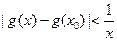 对任意
对任意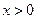 成立.
成立.
证法二 假设存在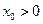 ,使
,使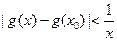 对任意
对任意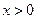 成立,
成立,
由(1)知,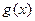 的最小值是
的最小值是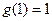 ,
,
又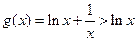 ,而
,而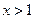 时,
时,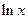 的值域为
的值域为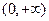 ,
,
∴当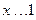 时,
时,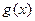 的值域为
的值域为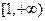 ,
,
从而可以取一个值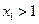 ,使
,使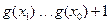 ,即
,即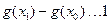 ,
,
∴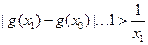 ,这与假设矛盾.
,这与假设矛盾.
∴不存在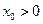 ,使
,使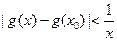 对任意
对任意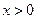 成立.
成立.



 20
20