三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.解答写在答题卡的制定区域内.
(16)(本小题满分13分)
在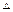 ABC中,a,b,c分别为内角A,B,C所对的边长,a=
ABC中,a,b,c分别为内角A,B,C所对的边长,a=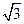 ,b=
,b=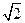
 ,
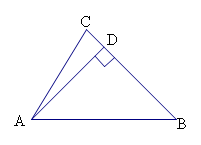
,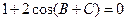 ,求边BC上的高.
,求边BC上的高.
(16)解:∵A+B+C=180°,所以B+C=A,
又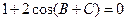 ,∴
,∴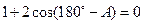 ,
,
即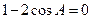 ,
, ,
,
又0°<A<180°,所以A=60°.
在△ABC中,由正弦定理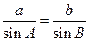 得
得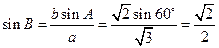 ,
,
又∵ ,所以B<A,B=45°,C=75°,
,所以B<A,B=45°,C=75°,
∴BC边上的高AD=AC·sinC=
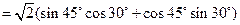
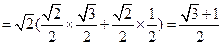 .
.
(17)(本小题满分13分)
设直线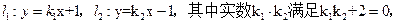
(I)证明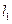 与
与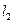 相交;
相交;
(II)证明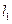 与
与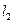 的交点在椭圆
的交点在椭圆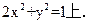
(18)(本小题满分13分)
设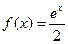 ,其中
,其中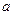 为正实数.
为正实数.
(Ⅰ)当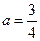 时,求
时,求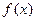 的极值点;
的极值点;
(Ⅱ)若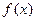 为
为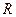 上的单调函数,求
上的单调函数,求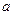 的取值范围.
的取值范围.
(19)(本小题满分13分)
如图,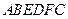 为多面体,平面
为多面体,平面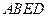 与平面
与平面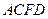 垂直,点
垂直,点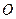 在线段
在线段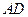 上,
上,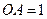 ,
,
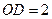 ,
,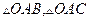 ,
,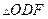 都是正三角形。
都是正三角形。
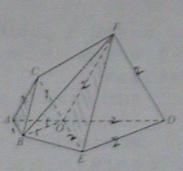
(Ⅰ)证明直线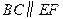 ;
;
(Ⅱ)求棱锥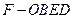 的体积.
的体积.
(20)(本小题满分10分)
某地最近十年粮食需求量逐年上升, 下表是部分统计数据:
下表是部分统计数据:
年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程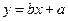 ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量。
(21)(本小题满分13分)
在数1和100之间插入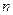 个实数,使得这
个实数,使得这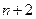 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这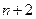 个数的乘积记作
个数的乘积记作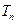 ,再令
,再令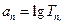
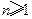 .
.
(Ⅰ)求数列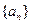 的通项公式;
的通项公式;
(Ⅱ)设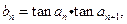 求数列
求数列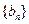 的前
的前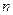 项和
项和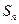 .
.