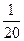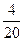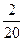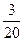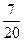12.已知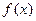 为奇函数,
为奇函数,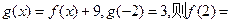 .
.
答案:6
13.设向量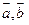 满足
满足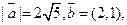 且
且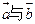 的方向相反,则
的方向相反,则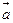 的坐标为 .
的坐标为 .
答案: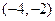
14.设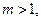 在约束条件
在约束条件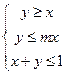 下,目标函数
下,目标函数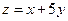 的最大值为4,则
的最大值为4,则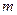 的值为 .
的值为 .
答案:3
15.已知圆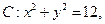 直线
直线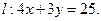
(1)圆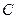 的圆心到直线
的圆心到直线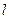 的距离为 .
的距离为 .
(2) 圆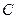 上任意一点
上任意一点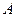 到直线
到直线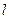 的距离小于2的概率为 .
的距离小于2的概率为 .
答案:5,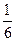
(2)由(1)可知圆心到直线的距离为5,要使圆上点到直线的距离小于2,即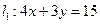 与圆相交所得劣弧上,由半径为
与圆相交所得劣弧上,由半径为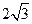 ,圆心到直线的距离为3可知劣弧所对圆心角为
,圆心到直线的距离为3可知劣弧所对圆心角为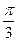 ,故所求概率为
,故所求概率为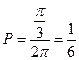 .
.
16、给定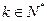 ,设函数
,设函数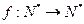 满足:对于任意大于
满足:对于任意大于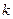 的正整数
的正整数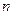 ,
,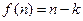
(1)设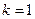 ,则其中一个函数
,则其中一个函数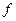 在
在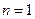 处的函数值为 ;
处的函数值为 ;
(2)设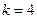 ,且当
,且当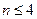 时,
时,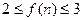 ,则不同的函数
,则不同的函数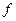 的个数为 。
的个数为 。
答案:(1)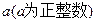 ,(2)16
,(2)16
(2)由题可知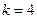 ,
,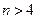 则
则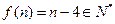 ,而
,而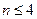 时,
时,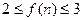 即
即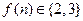 ,即
,即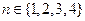 ,
,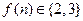 ,由乘法原理可知,不同的函数
,由乘法原理可知,不同的函数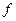 的个数为
的个数为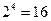 。
。
三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
在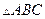 中,角
中,角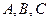 所对的边分别为
所对的边分别为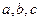 且满足
且满足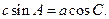
(I)求角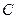 的大小;
的大小;
(II)求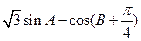 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角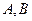 的大小.
的大小.
18.(本题满分12分)
某河流上的一座水力发电站,每年六月份的发电量Y(单位:万千瓦时)与该河上游在六月份的降雨量X(单位:毫米)有关.据统计,当X=70时,Y=460;X每增加10,Y增加5;已知近20年X的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(I)完成如下的频率分布表:
近20年六月份降雨量频率分布表
降雨量 | 70 | 110 | 140 | 160 | 200 | 220 |
频率 |
|
|
|
(II)假定今年六月份的降雨量与近20年六月份的降雨量的分布规律相同,并将频率视为概率,求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
解:(I)在所给数据中,降雨量为110毫米的有3个,为160毫米的有7个,为200毫米的有3个,故近20年六月份降雨量频率分布表为
降雨量 | 70 | 110 | 140 | 160 | 200 | 220 |
频率 |
|
|
|
|
|
|
(II)
故今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率为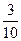 .
.