第Ⅱ卷
二.填空题:本大题共4小题,每小题5分,共20分.
(13)已知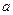 是第二象限的角,
是第二象限的角,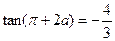 ,则
,则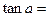 .
.
【答案】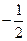
【命题意图】本试题主要考查三角函数的诱导公式、正切的二倍角公式和解方程,考查考生的计算能力.
【解析】由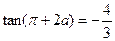 得
得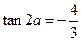 ,又
,又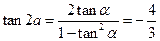 ,解得
,解得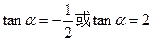 ,又
,又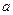 是第二象限的角,所以
是第二象限的角,所以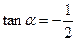 .
.
(14)若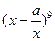 的展开式中
的展开式中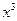 的系数是
的系数是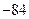 ,则
,则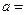 .
.
【答案】1
【命题意图】本试题主要考查二项展开式的通项公式和求指定项系数的方法.
【解析】展开式中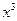 的系数是
的系数是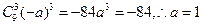 .
.
(15)已知抛物线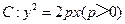 的准线为
的准线为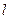 ,过
,过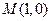 且斜率为
且斜率为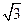 的直线与
的直线与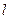 相交于点
相交于点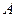 ,与
,与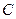 的一个交点为
的一个交点为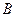 .若
.若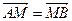 ,则
,则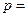 .
.
【答案】2
【命题意图】本题主要考查抛物线的定义与性质.
【解析】过B作BE垂直于准线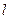 于E,∵
于E,∵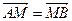 ,∴M为中点,∴
,∴M为中点,∴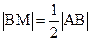 ,又斜率为
,又斜率为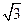 ,
,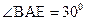 ,∴
,∴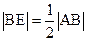 ,∴
,∴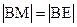 ,∴M为抛物线的焦点,∴
,∴M为抛物线的焦点,∴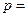 2.
2.
(16)已知球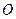 的半径为4,圆
的半径为4,圆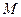 与圆
与圆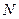 为该球的两个小圆,
为该球的两个小圆,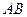 为圆
为圆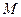 与圆
与圆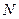 的公共弦,
的公共弦,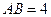 .若
.若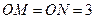 ,则两圆圆心的距离
,则两圆圆心的距离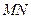
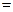 .
.
【答案】3 
【命题意图】本试题主要考查球的截面圆的性质,解三角形问 题.
题.
【解析】设E为AB的中点,则O,E,M,N四点共面,如图,∵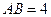 ,所以
,所以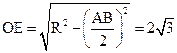 ,∴
,∴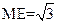 ,由球的截面性质,有
,由球的截面性质,有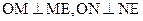 ,∵
,∵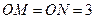 ,所以
,所以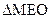 与
与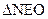 全等,所以MN被OE垂直平分,在直角三角形中,由面积相等,可得,
全等,所以MN被OE垂直平分,在直角三角形中,由面积相等,可得,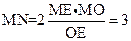
三.解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分10分)
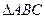 中,
中,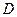 为边
为边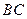 上的一点,
上的一点,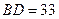 ,
,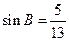 ,
,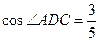 ,求
,求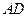 .
.
【命题意图】本试题主要考查同角三角函数关系、两角和差公式和正弦定理在解三角形中的应用,考查考生对基础知识、基本技能的掌握情况.
【参考答案】

【点评】三角函数与解三角形的综合性问题,是近几年高考的热点,在高考试题中频繁出现.这类题型难度比较低,一般出现在17或18题,属于送分题,估计以后这类题型仍会保留,不会有太大改变.解决此类问题,要根据已知条件,灵活运用正弦定理或余弦定理,求边角或将边角互化.
(18)(本小题满分12分)
已知数列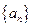 的前
的前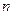 项和
项和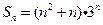 .
.
(Ⅰ)求
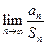 ;
;
(Ⅱ)证明: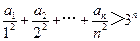 .
.
【命题意图】本试题主要考查数列基本公式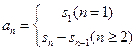 的运用,数列极限和数列不等式的证明,考查考生运用所学知识解决问题的能力.
的运用,数列极限和数列不等式的证明,考查考生运用所学知识解决问题的能力.
【参考答案】
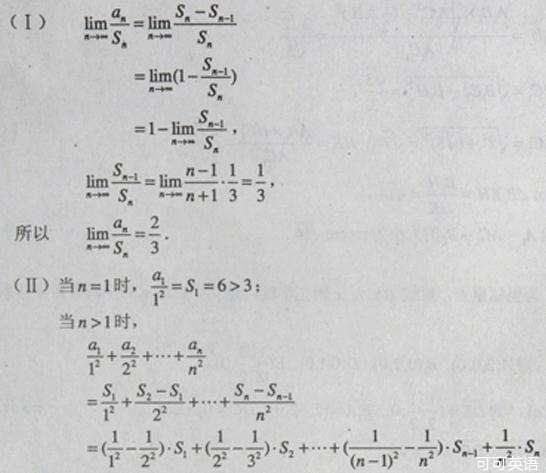
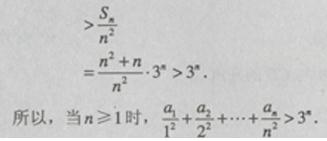
【点评】2010年高考数学全国I、Ⅱ这两套试卷都将数列题前置,一改往年的将数列结合不等式放缩法问题作为押轴题的命题模式,具有让考生和一线教师重视教材和基础知识、基本方法基本技能,重视两纲的导向作用,也可看出命题人在有意识降低难度和求变的良苦用心.
估计以后的高考,对数列的考查主要涉及数列的基本公式、基本性质、递推数列、数列求和、数列极限、简单的数列不等式证明等,这种考查方式还要持续.
(19)如图,直三棱柱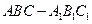 中,
中,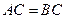 ,
,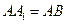 ,
,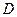 为
为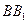 的中点,
的中点,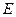 为
为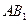 上的一点,
上的一点,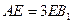 .
.
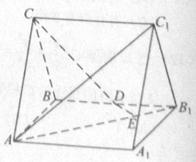
(Ⅰ)证明: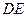 为异面直线
为异面直线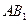 与
与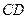 的公垂线;
的公垂线;
(Ⅱ)设异 面直线
面直线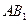 与
与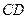 的夹角为45°,求二面角
的夹角为45°,求二面角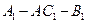 的大小.
的大小.
【命题意图】本试题主要考查空间的线面关系与空间角的求解,考查考生的空间想象与推理计算的能力.
【参考答案】




【点评】三垂线定理是立体几何的最重要定理之 一,是高考的的热点,它是处理线线垂直问题的有效方法,同时它也是确定二面角的平面角的主要手段.通过引入空间向量,用向量代数形式来处理立体几何问题,淡化了传统几何中的“形”到“形”的推理方法,从而降低了思维难度,使解题变得程序化,这是用向量解立体几何问题的独到之处.
一,是高考的的热点,它是处理线线垂直问题的有效方法,同时它也是确定二面角的平面角的主要手段.通过引入空间向量,用向量代数形式来处理立体几何问题,淡化了传统几何中的“形”到“形”的推理方法,从而降低了思维难度,使解题变得程序化,这是用向量解立体几何问题的独到之处.












