第Ⅰ卷(共60分)
一、选择题:本大题共l0小题.每小题5分,共50分在每小题给出的四个选项中,只有一项是满足题目要求的.
1.设集合 M ={x|(x+3)(x-2)<0},N ={x|1≤x≤3},则M∩N =
(A)[1,2) (B)[1,2] (C)( 2,3] (D)[2,3]
【答案】A
【解析】因为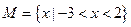 ,所以
,所以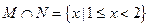 ,故选A.
,故选A.
2.复数z=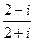 (
(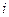 为虚数单位)在复平面内对应的点所在象限为
为虚数单位)在复平面内对应的点所在象限为
(A)第一象限 (B)第二象限 (C )第三象限 (D)第四象限
)第三象限 (D)第四象限
【答案】D
【解析】因为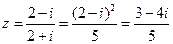 ,故复数z对应点在第四象限,选D.
,故复数z对应点在第四象限,选D.
3.若点(a,9)在函数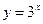 的图象上,则tan=
的图象上,则tan=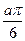 的值为
的值为
(A)0 (B) 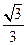 (C) 1 (D)
(C) 1 (D) 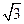
【答案】D
【解析】由题意知:9=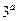 ,解得
,解得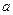 =2,所以
=2,所以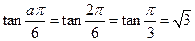 ,故选D.
,故选D.
4.曲线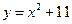 在点P(1,12)处的切线与y轴交点的纵坐标是
在点P(1,12)处的切线与y轴交点的纵坐标是
(A)-9 (B)-3 (C)9 (D)15

5.已知a,b,c∈R,命题“若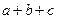 =3,则
=3,则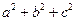 ≥3”,的否命题是
≥3”,的否命题是
(A)若a+b+c≠3,则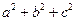 <3
<3
(B)若a+b+c=3,则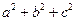 <3
<3
(C)若a+b+c≠3,则
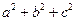 ≥3
≥3
(D)若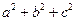 ≥3,则a+b+c=3
≥3,则a+b+c=3
【答案】A
【解析】命题“若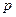 ,则
,则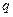 ”的否命题是“若
”的否命题是“若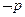 ,则
,则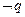 ”,故选A.
”,故选A.
6.若函数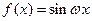 (ω>0)在区间
(ω>0)在区间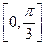 上单调递增,在区间
上单调递增,在区间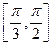 上单调递减,则ω=
上单调递减,则ω=
(A)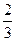 (B)
(B)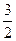 (C
(C )
) 2 (D)3
2 (D)3
【答 案】B
案】B
【解析】由题意知,函数 在
在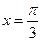 处取得最大值1,所以1=sin
处取得最大值1,所以1=sin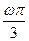 ,故选B.
,故选B.
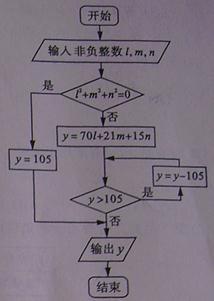
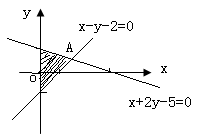 7.设变量x,y满足约束条件
7.设变量x,y满足约束条件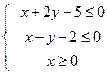 ,则目标函数
,则目标函数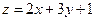 的最大值为
的最大值为
(A)11 (B)10  (C)9 (D)8.5
(C)9 (D)8.5
【答案】B
【解析】画出平面区域表示的可行域如图所示,当直线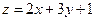 平移至点A(3,1)时, 目标函数
平移至点A(3,1)时, 目标函数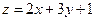 取得最大值为10,故选B.
取得最大值为10,故选B.
8.某产品的广告费用x与销售额y的统计数据如下表

根据上表可得回归方程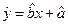 中的
中的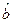 为9.4,据此模型预报广告费用为6万元时销售额为
为9.4,据此模型预报广告费用为6万元时销售额为
(A)63.6万元 (B)65.5万元 (C)67.7万元 (D)72.0万元
【答案】B
【解析】由表可计算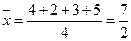 ,
,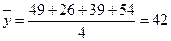 ,因为点
,因为点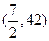 在回归直线
在回归直线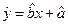 上,且
上,且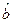 为9.4,所以
为9.4,所以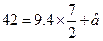 , 解得
, 解得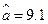 ,故回归方程为
,故回归方程为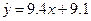 , 令x=6得
, 令x=6得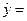 65.5,选B.
65.5,选B.
9.设M(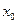 ,
,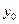 )为
)为 抛物线C:
抛物线C: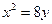 上一点,F为抛物线C的焦点,以F为圆心、
上一点,F为抛物线C的焦点,以F为圆心、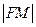 为半径的圆和抛物线C的准线相交,则
为半径的圆和抛物线C的准线相交,则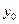 的取值范围是
的取值范围是
(A)(0,2) (B)[0,2] (C)(2,+∞) (D)[2,+∞)
【答案】C
【解析】设圆的半径为r,因为F(0,2)是圆心, 抛物线C的准线方程为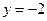 ,由圆与准线相切知4<r,因为点M(
,由圆与准线相切知4<r,因为点M(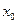 ,
,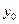 )为
)为 抛物线C:
抛物线C: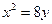 上一点,所以有
上一点,所以有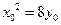 ,又点M(
,又点M(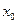 ,
,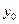 )在圆
)在圆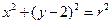 ,所以
,所以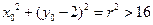 ,所以
,所以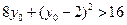 ,即有
,即有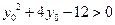 ,解得
,解得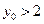 或
或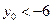 , 又因为
, 又因为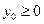 , 所以
, 所以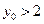 , 选C.
, 选C.
的距离为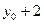 ,
,
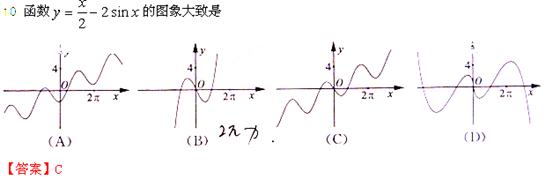
【解析】因为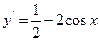 ,所
,所 以令
以令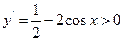 ,得
,得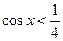 ,此时原函数是增函数;令
,此时原函数是增函数;令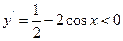 ,得
,得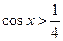 ,此时原函数是减函数,结合余弦函
,此时原函数是减函数,结合余弦函 数图象,可得选C正确.
数图象,可得选C正确.
11.下图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱 柱,其正(主)视图、俯视图如下图;②存在四棱柱,其正(主)视图、俯视图如下图;③存在圆柱,其正(主)视图、俯视图如下图.
柱,其正(主)视图、俯视图如下图;②存在四棱柱,其正(主)视图、俯视图如下图;③存在圆柱,其正(主)视图、俯视图如下图. 其中真命题的个数是
其中真命题的个数是
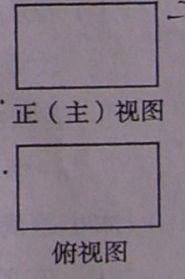
(A)3 (B)2 (C)1 (D)0
【答案】A
【解析】对于①,可以是放倒的三棱柱;容易判断②③可以.
12.设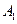 ,
,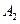 ,
,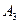 ,
,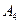 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若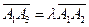 (λ∈R),
(λ∈R),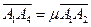 (μ∈R),且
(μ∈R),且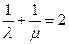 ,则称
,则称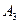 ,
,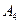 调和分割
调和分割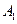 ,
, ,已知点C(c,o),D(d,O)
,已知点C(c,o),D(d,O) (c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是
(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是
(A)C可能是线段AB的中点
(B)D可能是线段AB的中点
(C)C,D可能同时在线段AB上
(D) C,D不可能同时在线段AB的延长线上
【答案】D
【解析】由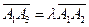 (λ∈R),
(λ∈R),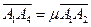 (μ∈R)知:四点
(μ∈R)知:四点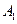 ,
,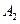 ,
,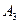 ,
,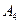 在同一条直线上,
在同一条直线上,
因为C,D调和分割点A,B,所以A,B,C,D四点在同一直线上,且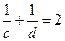 , 故选D.
, 故选D.












