第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)若复数z满足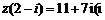 为虚数单位),则
为虚数单位),则 为
为
(A)3+5i (B)3-5i(C)-3+5i (D)-3-5i
【解析】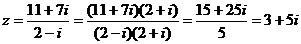 .故选A.
.故选A.
【答案】A
(2)已知全集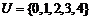 ,集合
,集合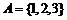 ,
,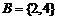 ,则
,则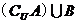 为
为
(A){1,2,4}(B){2,3,4}(C){0,2,4}(D){0,2,3,4}
【解析】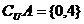 ,所以
,所以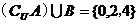 ,选C.
,选C.
【答案】C
(3)函数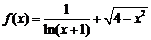 的定义域为
的定义域为
(A)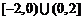 (B)
(B)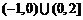 (C)
(C)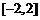 (D)
(D)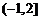
【解析】要使函数有意义则有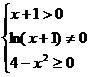 ,即
,即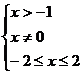 ,即
,即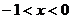 或
或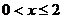 ,选B.
,选B.
【答案】B
(4)在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是
(A)众数 (B)平均数 (C)中位数 (D)标准差
【解析】设A样本的数据为变量为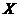 ,B样本的数据为变量为
,B样本的数据为变量为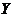 ,则满足
,则满足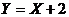 ,根据方差公式可得
,根据方差公式可得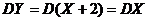 ,所以方差相同,标准差也相同,选D.
,所以方差相同,标准差也相同,选D.
【答案】D
(5)设命题p:函数 的最小正周期为
的最小正周期为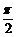 ;命题q:函数
;命题q:函数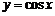 的图象关于直线
的图象关于直线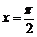 对称.则下列判断正确的是
对称.则下列判断正确的是
(A)p为真 (B)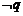 为假 (C)
为假 (C)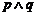 为假 (D)
为假 (D)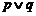 为真
为真
【解析】函数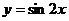 的周期为
的周期为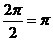 ,所以命题
,所以命题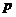 为假;函数
为假;函数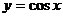 的对称轴为
的对称轴为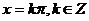 ,所以命题
,所以命题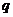 为假,所以
为假,所以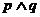 为假,选C.
为假,选C.
【答案】C
(6)设变量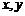 满足约束条件
满足约束条件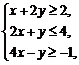 则目标函数
则目标函数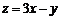 的取值范围是
的取值范围是
(A)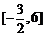 (B)
(B)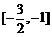 (C)
(C)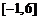 (D)
(D)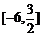
【解析】做出不等式所表示的区域如图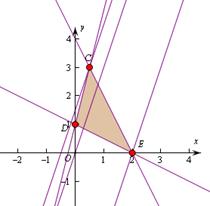 ,由
,由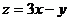 得
得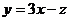 ,平移直线
,平移直线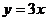 ,由图象可知当直线经过点
,由图象可知当直线经过点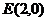 时,直线
时,直线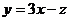 的截距最小,此时
的截距最小,此时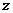 最大为
最大为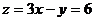 ,当直线经过
,当直线经过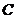 点时,直线截距最大,此时
点时,直线截距最大,此时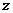 最小,由
最小,由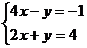 ,解得
,解得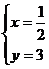 ,此时
,此时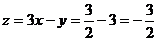 ,所以
,所以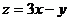 的取值范围是
的取值范围是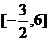 ,选A.
,选A.
【答案】A
(7)执行右面的程序框图,如果输入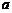 =4,那么输出的n的值为
=4,那么输出的n的值为
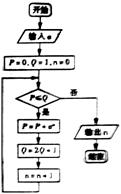
(A)2 (B)3 (C)4 (D)5
【解析】当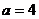 时,第一次
时,第一次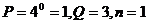 ,第二次
,第二次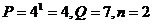 ,第三次
,第三次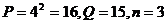 ,此时
,此时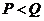 不满足,输出
不满足,输出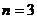 ,选B.
,选B.
【答案】B
(8)函数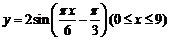 的最大值与最小值之和为
的最大值与最小值之和为
(A)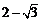 (B)0 (C)-1 (D)
(B)0 (C)-1 (D)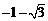
【解析】因为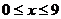 ,所以
,所以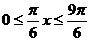 ,
,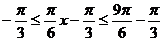 ,即
,即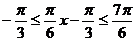 ,所以当
,所以当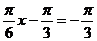 时,最小值为
时,最小值为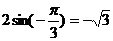 ,当
,当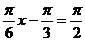 时,最大值为
时,最大值为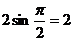 ,所以最大值与最小值之和为
,所以最大值与最小值之和为 ,选A.
,选A.
【答案】A
(9)圆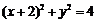 与圆
与圆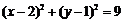 的位置关系为
的位置关系为
(A)内切 (B)相交 (C)外切 (D)相离
【解析】两圆的圆心分别为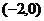 ,
,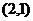 ,半径分别为
,半径分别为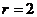 ,
,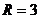 两圆的圆心距离为
两圆的圆心距离为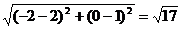 ,则
,则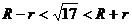 ,所以两圆相交,选B.
,所以两圆相交,选B.
【答案】B
(10)函数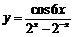 的图象大致为
的图象大致为

【解析】函数为奇函数,所以图象关于原点对称,排除A,令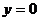 得
得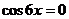 ,所以
,所以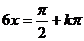 ,
,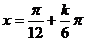 ,函数零点有无穷多个,排除C,且
,函数零点有无穷多个,排除C,且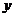 轴右侧第一个零点为
轴右侧第一个零点为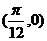 ,又函数
,又函数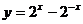 为增函数,当
为增函数,当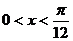 时,
时,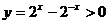 ,
,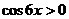 ,所以函数
,所以函数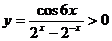 ,排除B,选D.
,排除B,选D.
【答案】D
(11)已知双曲线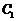 :
: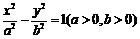 的离心率为2.若抛物线
的离心率为2.若抛物线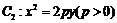 的焦点到双曲线
的焦点到双曲线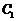 的渐近线的距离为2,则抛物线
的渐近线的距离为2,则抛物线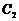 的方程为
的方程为
(A) 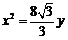 (B)
(B) 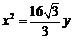 (C)
(C)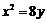 (D)
(D)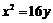
【解析】抛物线的焦点 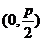 ,双曲线的渐近线为
,双曲线的渐近线为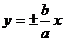 ,不妨取
,不妨取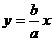 ,即
,即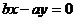 ,焦点到渐近线的距离为
,焦点到渐近线的距离为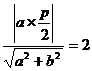 ,即
,即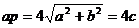 ,所以
,所以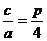 双曲线的离心率为
双曲线的离心率为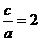 ,所以
,所以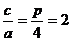 ,所以
,所以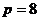 ,所以抛物线方程为
,所以抛物线方程为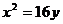 ,选D.
,选D.
【答案】D
(12)设函数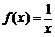 ,
,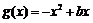 .若
.若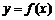 的图象与
的图象与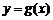 的图象有且仅有两个不同的公共点
的图象有且仅有两个不同的公共点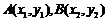 ,则下列判断正确的是
,则下列判断正确的是
(A)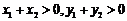 (B)
(B)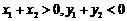
(C)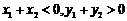 (D)
(D)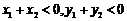
【解析】方法一:在同一坐标系中分别画出两个函数的图象,要想满足条件,则有如图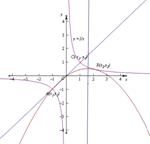 ,做出点A关于原点的对称点C,则C点坐标为
,做出点A关于原点的对称点C,则C点坐标为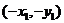 ,由图象知
,由图象知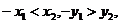 即
即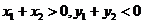 ,故答案选B.
,故答案选B.
方法二:设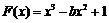 ,则方程
,则方程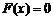 与
与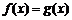 同解,故其有且仅有两个不同零点
同解,故其有且仅有两个不同零点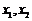 .由
.由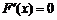 得
得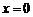 或
或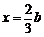 .这样,必须且只须
.这样,必须且只须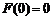 或
或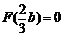 ,因为
,因为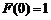 ,故必有
,故必有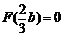 由此得
由此得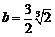 .不妨设
.不妨设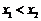 ,则
,则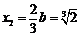 .所以
.所以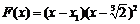 ,比较系数得
,比较系数得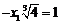 ,故
,故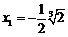 .
.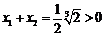 ,由此知
,由此知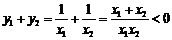 ,故答案为B.
,故答案为B.
【答案】B












