一、选择题(本大题共8个小题,每小题只有一个选项符合题目要求,每小题3分,满分24分)
1.(3分)(2013•红河州)﹣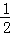 的倒数是( )
的倒数是( )
A. ﹣2 B. 2 C. ﹣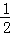 D.
D.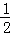
考点: 倒数.
专题: 计算题.
分析: 乘积是1的两数互为倒数,由此可得出答案.
解答: 解:﹣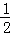 的倒数为﹣2.
的倒数为﹣2.
故选A.
点评: 此题考查了倒数的定义,属于基础题,注意掌握乘积是1的两数互为倒数.
2.(3分)(2013•红河州)如图是某个几何体的三视图,该几何体是( )
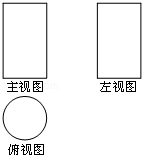
A. 正方体 B. 圆柱 C. 圆锥 D. 球
考点: 由三视图判断几何体.
分析: 首先根据俯视图将正方体淘汰掉,然后跟主视图和左视图将圆锥和球淘汰;
解答: 解:∵俯视图是圆,
∴排除A,
∵主视图与左视图均是长方形,
∴排除C、D
故选B.
点评: 此题主要考查了简单几何体的三视图,用到的知识点为:三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形.
3.(3分)(2013•红河州)下列运算正确的是( )
A. a+a=a2 B. a6÷a3=a2 C. (π﹣3.14)0=0 D.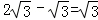
考点: 二次根式的加减法;合并同类项;同底数幂的除法;零指数幂.
专题: 计算题.
分析: A、合并同类项得到结果,即可作出判断;
B、利用同底数幂的除法法则计算得到结果,即可作出判断;
C、利用零指数幂法则计算得到结果,即可作出判断;
D、合并同类二次根式得到结果,即可作出判断.
解答: 解:A、a+a=2a,本选项错误;
B、a6÷a3=a3,本选项错误;
C、(π﹣3.14)0=1,本选项错误;
D、2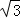 ﹣
﹣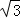 =
=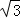 ,本选项正确,
,本选项正确,
故选D
点评: 此题考查了二次根式的加减法,合并同类项,同底数幂的除法,以及零指数幂,熟练掌握运算法则是解本题的关键.
4.(3分)(2013•红河州)不等式组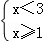 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A.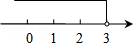 B.
B.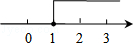 C.
C.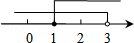 D.
D.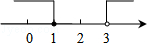
考点: 在数轴上表示不等式的解集.
分析: 把不等式组中每一个不等式的解集,表示在数轴上即可
解答: 解:不等式组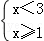 的解集在数轴上表示
的解集在数轴上表示
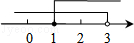 .
.
故选C.
点评: 把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
5.(3分)(2013•红河州)计算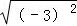 的结果是( )
的结果是( )
A. ﹣3 B. 3 C. ﹣9 D. 9
考点: 二次根式的性质与化简
专题: 计算题.
分析: 原式利用二次根式的化简公式计算即可得到结果.
解答: 解:原式=|﹣3|=3.
故选B
点评: 此题考查了二次根式的性质与化简,熟练掌握二次根式的化简公式是解本题的关键.
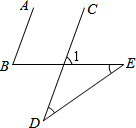
6.(3分)(2013•红河州)如图,AB∥CD,∠D=∠E=35°,则∠B的度数为( )
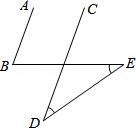
A. 60° B. 65° C. 70° D. 75°
考点: 平行线的性质;三角形的外角性质.
分析: 根据 三角形的一个外角等于与它不相邻的两个内角的和求出∠1,再根据两直线平行,同位角相等解答.
解答: 解:∵∠D=∠E=35°,
∴∠1=∠D+∠E=35°+35°=70°,
∵AB∥CD,
∴∠B=∠1=70°.
故选C.
点评: 本题考查了平行线的性质,三角形的外角性质,熟记各性质并准确识图是解题的关键.
7.(3分)(2013•红河州)在平面直角坐标系中,已知点P的坐标是(﹣1,﹣2),则点P关于原点对称的点的坐标是( )
A. (﹣1,2) B. (1,﹣2) C. (1,2) D. (2,1)
考点: 关于原点对称的点的坐标.
分析: 平面直角坐标系中任意一点P(x,y),关于原点的对称点是(﹣x,﹣y),据此即可求得点P关于原点的对称点的坐标.
解答: 解:∵点P关于x轴的对称点坐标为(﹣1,﹣2),
∴点P关于原点的对称点的坐标是(1,2).
故选:C.
点评: 此题主要考查了关于原点对称点的坐标性质,这一类题目是需要识记的基础题,要熟悉关于原点对称点的横纵坐标变化规律.
8.(3分)(2013•红河州)如图,AB是⊙O的直径,点C在⊙O上,弦BD平分∠ABC,则下列结论错误的是( )
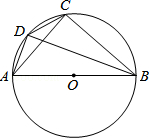
A. AD=DC B.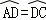 C. ∠ADB=∠ACB D. ∠DAB=∠CBA
C. ∠ADB=∠ACB D. ∠DAB=∠CBA
考点: 圆周角定理;圆心角、弧、弦的关系.
专题: 探究型.
分析: 根据圆周角定理,圆心角、弧、弦的关系对各选项进行逐一分析即可.
解答: 解:∵弦BD平分∠ABC,∴∠DBC=∠ABD,∴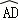 =
=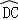 ,AD=DC,故A、B正确;
,AD=DC,故A、B正确;
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,故C正确;
∵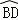 >
>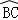 ,∴∠DAB>∠CBA,故D错误.
,∴∠DAB>∠CBA,故D错误.
故选D.
点评: 本题考查的是圆周角定理及圆心角、弧、弦的关系,熟知直径所对的圆周角是直角是解答此题的关键.












