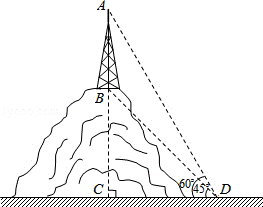
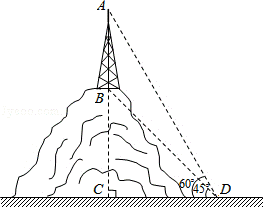
20.(6分)(2013•红河州)如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距塔AB的距离DC为100米,求手机信号中转塔AB的高度(结果保留根号).
考点: 解直角三角形的应用-仰角俯角问题.
分析: 先在Rt△BCD中,根据∠BDC=45°,得出BC=CD=100;再在Rt△ACD中,根据正切函数的定义,求出AC=100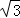 ,然后由AB=AC﹣BC即可求解.
,然后由AB=AC﹣BC即可求解.
解答: 解:由题意可知,△ACD与△BCD都是直角三角形.
在Rt△BCD中,∵∠BDC=45°,
∴BC=CD=100.
在Rt△ACD中,∵∠ADC=60°,CD=100,
∴tan∠ADC=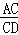 ,即
,即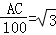 ,
,
∴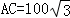 ,
,
∴AB=AC﹣BC=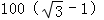 .
.
答:手机信号中转塔的高度为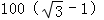 米.
米.
点评: 本题考查了解直角三角形的应用﹣仰角俯角问题,难度适中,解答本题的关键是借助仰角构造直角三角形并解直角三角形.
21.(6分)(2013•红河州)如图,正比例函数y1=x的图象与反比例函数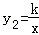 (k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(1)求反比例函数的解析式;
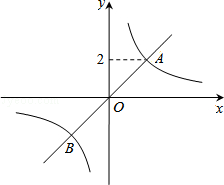
(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量x的取值范围.
考点: 反比例函数与一次函数的交点问题.
专题: 计算题.
分析: (1)设A(m,2),将A纵坐标代入正比例解析式求出m的值,确定出A坐标,代入反比例解析式求出k的值,即可确定出反比例解析式;
(2)联立两函数解析式求出B的坐标,由A与B横坐标,利用图象即可求出当y1>y2时,自变量x的取值范围.
解答: 解:(1)设A点的坐标为(m,2),代入y1=x得:m=2,
∴点A的坐标为(2,2),
∴k=2×2=4,
∴反比例函数的解析式为y2=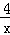 ;
;
(2)当y1=y2时,x=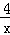 ,
,
解得:x=±2,
∴点B的坐标为(﹣2,﹣2),
则由图象可知,当y1>y2时,自变量x的取值范围是:﹣2<x<0或x>2.
点评: 此题考查了反比例函数与一次函数的交点问题,利用数形结合的思想,熟练掌握数形结合思想是解本题的关键.
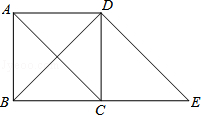
22.(7分)(2013•红河州)如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
考点: 正方形的性质;勾股定理;平行四边形的判定.
分析: (1)根据正方形的对边互相平行可得AD∥BC,即为AD∥CE,然后根据两组对边互相平行的四边形是平行四边形解答;
(2)根据正方形的四条边都相等,平行四边形的对边相等可得BC=AD=CE,再根据正方形的边长等于对角线的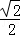 倍求出BC,然后求出BE即可.
倍求出BC,然后求出BE即可.
解答: 解:(1)四边形ACED是平行四边形.
理由如下:∵四边形ABCD是正方形,
∴AD∥BC,
即AD∥CE,
∵DE∥AC,
∴四边形ACED是平行四边形;
(2)由(1)知,BC=AD=CE=CD,
∵BD=8cm,
∴BC=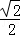 BD=
BD=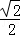 ×8=4
×8=4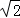 cm,
cm,
∴BE=BC+CE=4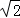 +4
+4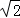 =8
=8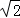 cm.
cm.
点评: 本题考查了正方形的性质,平行四边形的判定与性质,比较简单,熟练掌握各图形的性质是解题的关键.
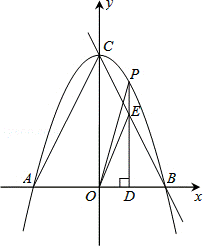
23.(9分)(2013•红河州)如图,抛物线y=﹣x2+4与x轴交于A、B两点,与y轴交于C点,点P是抛物线上的一个动点且在第一象限,过点P作x轴的垂线,垂足为D,交直线BC于点E.
(1)求点A、B、C的坐标和直线BC的解析式;
(2)求△ODE面积的最大值及相应的点E的坐标;
(3)是否存在以点P、O、D为顶点的三角形与△OAC相似?若存在,请求出点P的坐标,若不存在,请说明理由.
考点: 二次函数综合题
分析: (1)在抛物线解析式y=﹣x2+4中,令y=0,解方程可求得点A、点B的坐标;令x=0,可求得顶点C的坐标.已知点B、C的坐标,利用待定系数法求出直线BC的解析式;
(2)求出△ODE面积的表达式,利用二次函数的性质求出最大值,并确定点E的坐标;
(3)本问为存在型问题.因为△OAC与△OPD都是直角三角形,需要分类讨论:
①当△PDO∽△COA时,由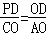 得PD=2OD,列方程求出点P的坐标;
得PD=2OD,列方程求出点P的坐标;
②当△PDO∽△AOC时,由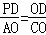 得OD=2PD,列方程求出点P的坐标.
得OD=2PD,列方程求出点P的坐标.
解答: 解:(1)在y=﹣x2+4中,当y=0时,即﹣x2+4=0,解得x=±2.
当x=0时,即y=0+4,解得y=4.
所以点A、B、C的坐标依次是A(﹣2,0)、B(2,0)、C(0,4).
设直线BC的解析式为y=kx+b(k≠0),
则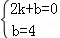 ,解得
,解得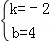 .
.
所以直线BC的解析式为y=﹣2x+4. …3分
(2)∵点E在直线BC上,
∴设点E的坐标为(x,﹣2x+4),
则△ODE的面积S可表示为: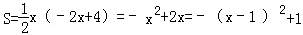 .
.
∴当x=1时,△ODE的面积有最大值1.
此时,﹣2x+4=﹣2×1+4=2,
∴点E的坐标为(1,2). …5分
(3)存在以点P、O、D为顶点的三角形与△OAC相似,理由如下:
设点P的坐标为(x,﹣x2+4),0<x<2.
因为△OAC与△OPD都是直角三角形,分两种情况:
①当△PDO∽△COA时,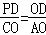 ,
,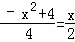 ,
,
解得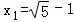 ,
,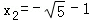 (不符合题意,舍去).
(不符合题意,舍去).
当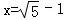 时,
时,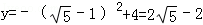 .
.
此时,点P的坐标为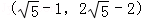 .
.
②当△PDO∽△AOC时,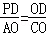 ,
,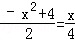 ,
,
解得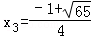 ,
,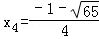 (不符合题意,舍去).
(不符合题意,舍去).
当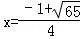 时,
时,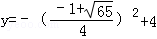 =
=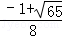 .
.
此时,点P的坐标为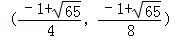 .
.
综上可得,满足条件的点P有两个: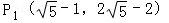 ,
,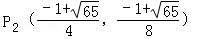 . …9分.
. …9分.
点评: 本题是二次函数压轴题,考查了二次函数的图象与性质、待定系数法、二次函数的最值、相似三角形、解方程等知识点,难度不大.第(3)问是存在型问题,可能存在两种符合条件的情况,需要分类讨论,避免漏解.












