二、填空题（本题有6个小题，每小题3分，共18分）

11．（3分）（2013•黄石）分解因式：3x2﹣27=　3（x+3）（x﹣3）　．

考点： 提公因式法与公式法的综合运用．

分析： 观察原式3x2﹣27，找到公因式3，提出公因式后发现x2﹣9符合平方差公式，利用平方差公式继续分解．

解答： 解：3x2﹣27，

=3（x2﹣9），

=3（x+3）（x﹣3）．

点评： 本题主要考查提公因式法分解因式和利用平方差公式分解因式，熟记公式是解题的关键，难点在于要进行二次分解因式．

12．（3分）（2013•黄石）若关于x的函数y=kx2+2x﹣1与x轴仅有一个公共点，则实数k的值为　0或﹣1　．

考点： 抛物线与x轴的交点

分析： 令y=0，则关于x的方程kx2+2x﹣1=0只有一个根，所以k=0或根的判别式△=0，借助于方程可以求得实数k的值．

解答： 解：令y=0，则kx2+2x﹣1=0．

∵关于x的函数y=kx2+2x﹣1与x轴仅有一个公共点，

∴关于x的方程kx2+2x﹣1=0只有一个根．

①当k=0时，2x﹣1=0，即x=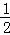，∴原方程只有一个根，∴k=0符号题意；

②当k≠0时，△=4+4k=0，

解得，k=﹣1．

综上所述，k=0或﹣1．

故答案是：0或﹣1．

点评： 本题考查了抛物线与x轴的交点．解题时，需要对函数y=kx2+2x﹣1进行分类讨论：一次函数和二次函数时，满足条件的k的值．

13．（3分）（2013•黄石）甲、乙玩猜数字游戏，游戏规则如下：有四个数字0、1、2、3，先由甲心中任选一个数字，记为m，再由乙猜甲刚才所选的数字，记为n．若m、n满足|m﹣n|≤1，则称甲、乙两人“心有灵犀”，则甲、乙两人“心有灵犀”的概率是　　．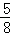

考点： 列表法与树状图法．

分析： 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与m、n满足|m﹣n|≤1的情况，再利用概率公式即可求得答案．

解答： 解：画树状图得：

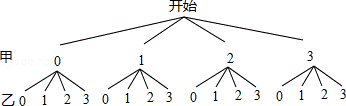
∵共有16种等可能的结果，m、n满足|m﹣n|≤1的有10种情况，

∴甲、乙两人“心有灵犀”的概率是：=．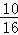

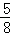故答案为：．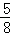

点评： 本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．

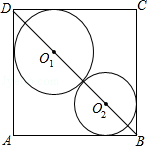
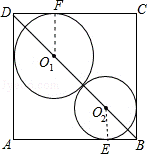
14．（3分）（2013•黄石）如图所示，在边长为3的正方形ABCD中，⊙O1与⊙O2外切，且⊙O2分别于DA、DC边外切，⊙O1分别与BA、BC边外切，则圆心距，O1O2为　　．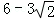

考点： 相切两圆的性质．

分析： 通过作辅助线构造直角三角形用勾股定理作为相等关系列方程求解．

解答： 解：如图所示，设⊙O1半径x，⊙O2半径y，

∵O1在∠ADC的平分线上；O2在∠ABC平分线上，而BD为正方形对角线，平分对角，

∴O1O2 在BD上，

∴∠ADB=∠DBA=45°，

∴DO1=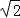x，BO2=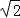y

则 DB=DO1+O1O2+O2B=x+y+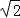（x+y）=3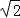

解得x+y=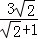=6﹣3．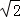

故答案为：6﹣3．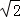

点评： 主要考查了相切两圆中的有关计算问题．解题方法主要是利用正方形的性质构造直角三角形，用勾股定理作为相等关系列方程求解．

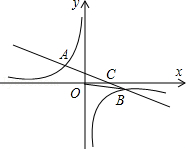
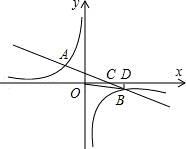
15．（3分）（2013•黄石）如图所示，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数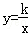（k≠0）的图象交于二、四象限的A、B两点，与x轴交于C点．已知A（﹣2，m），B（n，﹣2），tan∠BOC=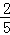，则此一次函数的解析式为　y=﹣x+3　．

考点： 反比例函数与一次函数的交点问题

专题： 计算题．

分析： 过点B作BD⊥x轴，在直角三角形BOD中，根据已知的三角函数值求出OD的长，得到点B的坐标，把点B的坐标代入反比例函数的解析式中，求出反比例函数的解析式，然后把点A的横坐标代入反比例函数的解析式中求出点A的坐标，最后分别把点A和点B的坐标代入一次函数解析式，求出a和b的值即可得到一次函数解析式．

解答： 解：过点B作BD⊥x轴，

在Rt△BOD中，∵tan∠BOC===，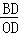

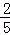∴OD=5，

则点B的坐标为（5，﹣2），

把点B的坐标为（5，﹣2）代入反比例函数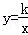（k≠0）中，

则﹣2=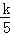，即k=﹣10，

∴反比例函数的解析式为y=﹣，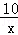

把A（﹣2，m）代入y=﹣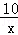中，m=5，

∴A的坐标为（﹣2，5），

把A（﹣2，5）和B（5，﹣2）代入一次函数y=ax+b（a≠0）中，

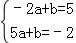得：，解得，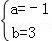

则一次函数的解析式为y=﹣x+3．

故答案为：y=﹣x+3．

点评： 此题考查了反比例函数和一次函数的交点问题，以及三角函数值，用待定系数法确定函数的解析式，是常用的一种解题方法．同学们要熟练掌握这种方法．

16．（3分）（2013•黄石）在计数制中，通常我们使用的是“十进位制”，即“逢十进一”，而计数制方法很多，如60进位制：60秒化为1分，60分化为1小时；24进位制：24小时化为一天；7进位制：7天化为1周等…而二进位制是计算机处理数据的依据．已知二进位制与十进位制比较如下表：

请将二进位制数10101010（二）写成十进位制数为　170　．

考点： 有理数的混合运算．

专题： 应用题．

分析： 根据二进制的意义即可花成十进制，从而求解．

解答： 解：10101010（二）=27+25+23+2=128+32+8+2=170．

故答案是：170．

点评： 本题考查了有理数的运算，理解二进制的意义是关键．

三、解答题（本题有9个小题，共72分）

17．（7分）（2013•黄石）计算：．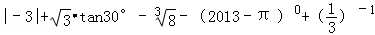

考点： 实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值．

专题： 计算题．

分析： 本题涉及零指数幂、负指数幂、特殊角的三角函数值、绝对值等考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．

解答： 解：原式=3+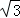×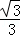﹣2﹣1+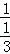

=3+1﹣2﹣1+3

=4．

点评： 本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握零指数幂、负指数幂、特殊角的三角函数值、绝对值等考点的运算．

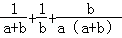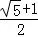18．（7分）（2013•黄石）先化简，再求值：，其中a=，b=．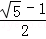

考点： 分式的化简求值

专题： 计算题．

分析： 本题中直接代数求值是非常麻烦的．本题的关键是正确进行分式的通分、约分，并准确代值计算．

解答： 解：原式=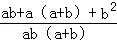

==

∵，；

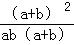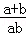
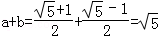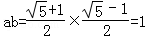∴原式=．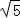

点评： 解答本题的关键是对分式进行化简，代值计算要仔细．

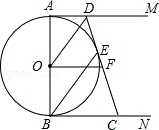
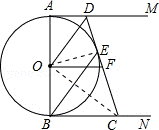
19．（7分）（2013•黄石）如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E是⊙O上一点，D是AM上一点，连接DE并延长交BN于点C，且OD∥BE，OF∥BN．

（1）求证：DE与⊙O相切；

（2）求证：OF=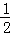CD．

考点： 切线的判定与性质；直角三角形斜边上的中线．

分析： （1）连接OE，由AM与圆O相切，利用切线的性质得到OA与AM垂直，即∠OAD=90°，根据OD与BE平行，利用两直线平行得到一对内错角相等，一对同位角相等，再由OB=OE，利用等边对等角得到一对角相等，等量代换得到一对角相等，再由OA=OE，OD为公共边，利用SAS得出三角形AOD与三角形EOD全等，利用全等三角形的对应角相等得到∠OED=90°，即OE垂直于ED，即可得证；

（2）连接OC，由CD与CB为圆的切线，利用切线的性质得到一对直角相等，由OB=OE，OC为公共边，利用HL得出两直角三角形全等，进而得到∠BOC=∠EOC，利用等量代换及平角定义得到∠COD=90°，即三角形COD为直角三角形，由OF与BN平行，AM与BN平行，得到三线平行，由O为AB的中的，利用平行线等分线段定理得到F为CD的中点，利用直角三角形斜边上的中线等于斜边的一半即可得证．

解答： 证明：（1）连接OE，

∵AM与圆O相切，

∴AM⊥OA，即∠OAD=90°，

∵OD∥BE，

∴∠AOD=∠ABE，∠EOD=∠OEB，

∵OB=OE，

∴∠ABE=∠OEB，

∴∠AOD=∠OEB，

∴∠AOD=∠EOD，

在△AOD和△EOD中，

，

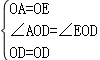∴△AOD≌△EOD（SAS），

∴∠OED=∠OAD=90°，

则DE为圆O的切线；

（2）在Rt△BCO和Rt△ECO中，

，

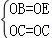∴Rt△BCO≌Rt△ECO，

∴∠BOC=∠EOC，

∵∠AOD=∠EOD，

∴∠DOC=∠EOD+∠EOC=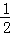×180°=90°，

∵AM、BN为圆O的切线，

∴AM⊥AB，BN⊥AB，

∴AM∥BN，

∵OF∥BN，

∴AM∥OF∥BN，

又O为AB的中点，

∴F为CD的中点，

则OF=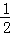CD．

点评： 此题考查了切线的判定与性质，全等三角形的判定与性质，平行线的性质，以及等腰三角形的性质，熟练掌握切线的判定与性质是解本题的关键．

20．（8分）（2013•黄石）解方程组：．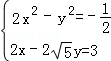

考点： 高次方程．

分析： 先由第二个方程得：x=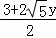 ③，再把③代入①得：2×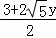（）2﹣y2=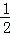，求出y1、y2，再代入③即可．

解答： 解：，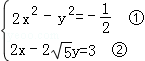

由②得：x=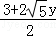 ③，

把③代入①得：2×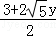（）2﹣y2=﹣，

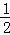化简得：9y2+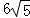y+5=0，

即：（3y+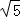）2=0

解得：y1=y2=，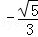

代入③得：x1=x2=，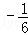

∴原方程组的解为．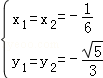

点评： 此题考查了高次方程，关键是利用代入法把高次方程转化成低次方程，注意结果有两种情况．

21．（8分）（2013•黄石）青少年“心理健康”问题越来越引起社会的关注，某中学为了了解学校600名学生的心理健康状况，举行了一次“心理健康”知识测试，并随即抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本，绘制了下面未完成的频率分布表和频率分布直方图．请回答下列问题：

（1）填写频率分布表中的空格，并补全频率分布直方图；

（2）若成绩在70分以上（不含70分）为心理健康状况良好，同时，若心理健康状况良好的人数占总人数的70%以上，就表示该校学生的心理健康状况正常，否则就需要加强心里辅导．请根据上述数据分析该校学生是否需要加强心里辅导，并说明理由．

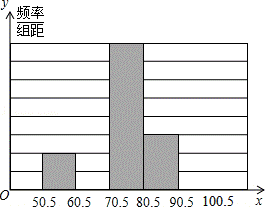
考点： 频数（率）分布直方图；频数（率）分布表．

分析： （1）由50.5～60.5的频数除以对应的频率求出样本的总人数，进而求出70.5～80.5的频率，90.5～100.5的频数，以及80.5～90.5的频率与频数，补全表格即可；

（2）该校学生需要加强心里辅导，理由为：求出70分以上的人数，求出占总人数的百分比，与70%比较大小即可．

解答： 解：（1）根据题意得：样本的容量为4÷0.08=50（人），

则70.5～80.5的频率为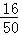=0.32，80.5～90.5的频率为1﹣（0.08+0.28+0.32+0.20）=0.12，频数为50×0.12=6；

分组 频数 频率

50.5～60.5 4 0.08

60.5～70.5 14 0.28

70.5～80.5 16 0.32

80.5～90.5 6 0.12

90.5～100.5 10 0.20

合计 50 1.00

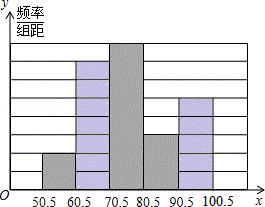
（2）该校学生需要加强心理辅导，理由为：

根据题意得：70分以上的人数为16+6+10=32（人），

∵心理健康状况良好的人数占总人数的百分比为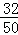×100%=64%＜70%，

∴该校学生需要加强心理辅导．

点评： 此题考查了频数（率）分布直方图，弄清题意是解本题的关键．

点击此处下载文档(rar格式，267.70KB)