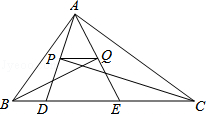
12．（4分）（2013•淄博）如图，△ABC的周长为26，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC=10，则PQ的长为（　　）

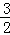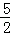A． B． C． 3 D． 4

考点： 三角形中位线定理；等腰三角形的判定与性质．

分析： 首先判断△BAE、△CAD是等腰三角形，从而得出BA=BE，CA=CD，由△ABC的周长为26，及BC=10，可得DE=6，利用中位线定理可求出PQ．

解答： 解：∵BQ平分∠ABC，BQ⊥AE，

∴△BAE是等腰三角形，

同理△CAD是等腰三角形，

∴点Q是AE中点，点P是AD中点（三线合一），

∴PQ是△ADE的中位线，

∵BE+CD=AB+AC=26﹣BC=26﹣10=16，

∴DE=BE+CD﹣BC=6，

∴PQ=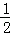DE=3．

故选C．

点评： 本题考查了三角形的中位线定理，解答本题的关键是判断出△BAE、△CAD是等腰三角形，利用等腰三角形的性质确定PQ是△ADE的中位线．

二、填空题：本题共5小题，满分20分．只要求填写最后结果，每小题填对得4分．

13．（4分）（2013•淄博）当实数a＜0时，6+a　＜　6﹣a（填“＜”或“＞”）．

考点： 不等式的性质．

分析： a＜0时，则a＜﹣a，在不等式两边同时加上6即可得到．

解答： 解：∵a＜0，

∴a＜﹣a，

在不等式两边同时加上6，得：6+a＜6﹣a．

故答案是：＜．

点评： 本题考查了不等式的基本性质，理解6+a＜6﹣a是如何变化得到的是关键．

14．（4分）（2013•淄博）请写出一个概率小于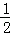的随机事件：　掷一个骰子，向上一面的点数为2　．

考点： 概率公式．

专题： 开放型．

分析： 根据概率公式P（A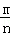）=，再结合本题题意，写出符合要求的事件即可，答案不唯一．

解答： 解：根据题意得：

概率小于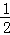的随机事件如：

掷一个骰子，向上一面的点数为2；

故答案为：掷一个骰子，向上一面的点数为2．

点评： 此题考查了概率公式，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．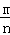

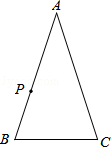
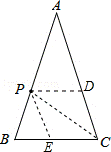
15．（4分）（2013•淄博）在△ABC中，P是AB上的动点（P异于A，B），过点P的一条直线截△ABC，使截得的三角形与△ABC相似，我们不妨称这种直线为过点P的△ABC的相似线．如图，∠A=36°，AB=AC，当点P在AC的垂直平分线上时，过点P的△ABC的相似线最多有　3　条．

考点： 相似三角形的判定；线段垂直平分线的性质．

专题： 新定义．

分析： 根据相似三角形的判定方法分别利用平行线以及垂直平分线的性质得出对应角相等即可得出．

解答： 解：当PD∥BC时，△APD∽△ABC，

当PE∥AC时，△BPE∽△BAC，

连接PC，

∵∠A=36°，AB=AC，点P在AC的垂直平分线上，

∴AP=PC，∠ABC=∠ACB=72°，

∴∠ACP=∠PAC=36°，

∴∠PCB=36°，

∴∠B=∠B，∠PCB=∠A，

∴△CPB∽△ACB，

故过点P的△ABC的相似线最多有3条．

故答案为：3．

点评： 此题主要考查了相似三角形的判定，正确掌握相似三角形的判定方法作出辅助线是解题关键．

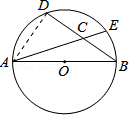
16．（4分）（2013•淄博）如图，AB是⊙O的直径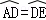，，AB=5，BD=4，则sin∠ECB=　　．

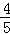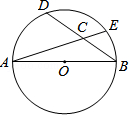
考点： 相似三角形的判定与性质；圆周角定理；锐角三角函数的定义

分析： 连接AD，在Rt△ABD中利用勾股定理求出AD，证明△DAC∽△DBA，利用对应边成比例的知识，可求出CD、AC，继而根据sin∠ECB=sin∠DCA=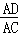即可得出答案．

解答： 解：连接AD，则∠ADB=90°，

在Rt△ABD中，AB=5，BD=4，

则AD=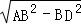=3，

∵，

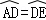∴∠DAC=∠DBA，

∴△DAC∽△DBA，

∴==，

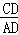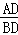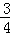∴CD=，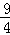

∴AC==，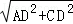

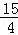∴sin∠ECB=sin∠DCA==．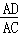

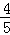故答案为：．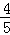

点评： 本题考查了相似三角形的判定与性质，解答本题的关键是作出辅助线，证明△DAC∽△DBA，求出CD、AD的长度，难度一般．

17．（4分）（2013•淄博）如下表，从左到右在每个小格中都填入一个整数，使得任意三个相邻格子所填整数之和都相等，则第2013个格子中的整数是　﹣2　．

考点： 规律型：数字的变化类．

分析： 根据三个相邻格子的整数的和相等列式求出a、c的值，再根据第9个数是﹣2可得b=﹣2，然后找出格子中的数每3个为一个循环组依次循环，在用2013除以3，根据余数的情况确定与第几个数相同即可得解．

解答： 解：∵任意三个相邻格子中所填整数之和都相等，

∴﹣4+a+b=a+b+c，

解得c=﹣4，

a+b+c=b+c+6，

解得a=6，

所以，数据从左到右依次为﹣4、6、b、﹣4、6、b，

第9个数与第三个数相同，即b=﹣2，

所以，每3个数“﹣4、6、﹣2”为一个循环组依次循环，

∵2013÷3=671，

∴第2013个格子中的整数与第3个格子中的数相同，为﹣2．

故答案为：﹣2．

点评： 此题主要考查了数字变化规律，仔细观察排列规律求出a、b、c的值，从而得到其规律是解题的关键．

三、解答题：本大题共7小题，共52分．解答要写出必要的文字说明、证明过程或演算步骤．

18．（5分）（2013•淄博）解方程组．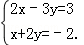

考点： 解二元一次方程组．

专题： 计算题．

分析： 先用加减消元法求出y的值，再用代入消元法求出x的值即可．

解答： 解：，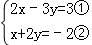

①﹣2×②得，﹣7y=7，解得y=﹣1；

把y=﹣1代入②得，x+2×（﹣1）=﹣2，解得x=0，

故此方程组的解为：．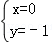

点评： 本题考查的是解二元一次方程组，熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键．

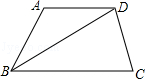
19．（5分）（2013•淄博）如图，AD∥BC，BD平分∠ABC．求证：AB=AD．

考点： 等腰三角形的判定与性质；平行线的性质．

专题： 证明题．

分析： 根据AD∥BC，可求证∠ADB=∠DBC，利用BD平分∠ABC和等量代换可求证∠ABD=∠ADB，然后即可得出结论．

解答： 证明：∵AD∥BC，

∴∠ADB=∠DBC，

∵BD平分∠ABC，

∴∠ABD=∠DBC，

∴∠ABD=∠ADB，

∴AB=AD．

点评： 此题主要考查学生对等腰三角形的判定与性质和平行线性质的理解和掌握，此题很简单，属于基础题．

点击此处下载文档(rar格式，211.89KB)