22.(8分)选取二次三项式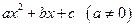 中的两项,配成完全平方式的过程叫配方。例如
中的两项,配成完全平方式的过程叫配方。例如
①选取二次项和一次项配方: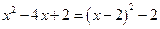 ;
;
②选取二次项和常数项配方: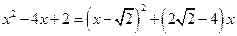 ,
,
或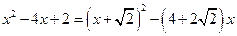
③选取一次项和常数项配方: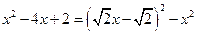
根据上述材料,解决下面问题:
(1)写出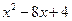 的两种不同形式的配方;
的两种不同形式的配方;
(2)已知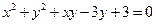 ,求
,求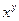 的值。
的值。
解析::(1)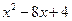 =x2-8x+16-16+4=(x-4)2-12
=x2-8x+16-16+4=(x-4)2-12
或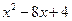 =(x-2)2-4x
=(x-2)2-4x
(2)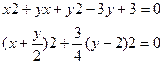
X=-1,y=2.因此xy=(-1)2=1
(四)(本题2个小题,共17分)
23.(8分)今年,6月12日为端午节。在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况。请根据小丽提供的信息,解答小华和小明提出的问题。

(1)小华的问题解答:
解析:(1)解:设实现每天800元利润的定价为x元/个,根据题意,得
(x-2)(500-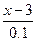 ×10)=800 .………………………(2分)
×10)=800 .………………………(2分)
整理得:x2-10x+24=0.
解之得:x1=4,x2=6.………………………(3分)
∵物价局规定,售价不能超过进价的240%,即2×240%=4.8(元).
∴x2=6不合题意,舍去,得x=4.
答:应定价4元/个,才可获得800元的利润.………………………(4分)
(2)解:设每天利润为W元,定价为x元/个,得
W=(x-2)(500-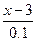 ×10)
×10)
=-100x2+1000x-1600
=-100(x-5)2+900.………………………(6分)
∵x≤5时W随x的增大而增大,且x≤4.8,
∴当x=4.8 时,W最大,
W最大=-100×(4.8-5)2+900=896>800 .………………………(7分)
故800元不是最大利润.当定价为4.8元/个时,每天利润最大.………………………(8分)
24.(9分)通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的。下面是一个案例,请补充完整。


 FF
FF
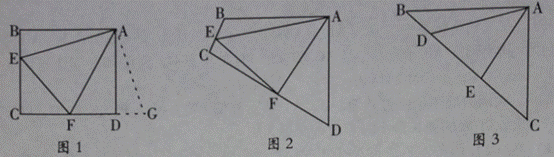
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由。
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合。
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线。
根据__SAS__________,易证△AFG≌_△AFE_______,得EF=BE+DF。
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°。若∠B、∠D都不是直角,则当∠B与∠D满足等量关系_互补___时,仍有EF=BE+DF。
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°。猜想BD、DE、EC应满足的等量关系,并写出推理过程。
解:BD2+EC2=DE2
解析:(1)SAS………………………(1分)
△AFE………………………(2分)
(2)∠B+∠D=180°………………………(4分)
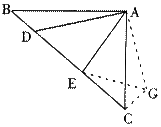 (3)解:BD2+EC2=DE2.………………………(5分)
(3)解:BD2+EC2=DE2.………………………(5分)
∵AB=AC,
∴把△ABD绕A点逆时针旋转90°至△ACG,可使AB与AC重合.
∵△ABC中,∠BAC=90°.
∴∠ACB+∠ACG=∠ACB+∠B=90°,即∠ECG=90°.
∴EC2+CG2=EG2.………………………(7分)
在△AEG与△AED中,
∠EAG=∠EAC+∠CAG=∠EAC+∠BAD=90°-∠EAD=45°=∠EAD,
又∵AD=AG,AE=AE,
∴△AEG≌△AED.
∴DE=EG.又∵CG=BD,
∴BD2+EC2=DE2.………………………(9分)
(五)(本题12分)
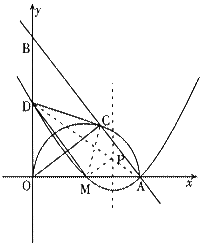
25.如图,在直角体系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3。取BO的中点D,连接CD、MD和OC。
(1)求证:CD是⊙M的切线;
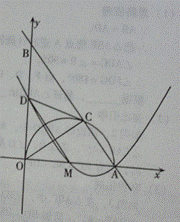
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使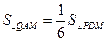 ?若存在,求出点Q的坐标;若不存在,请说明理由。
?若存在,求出点Q的坐标;若不存在,请说明理由。
解析:(1)证明:连结CM.
∵OA 为⊙M直径,
∴∠OCA=90°.
∴∠OCB=90°.
∵D为OB中点,
∴DC=DO.
∴∠DCO=∠DOC.………………………(1分)
∵MO=MC,
∴∠MCO=∠MOC.………………………(2分)
∴∠DCM=∠DCO+∠MCO=∠DOC+∠MOC=∠DOM=90°.………………………(3分)
 又∵点C在⊙M上,
又∵点C在⊙M上,
∴DC是⊙M的切线.………………………(4分)
(2)解:在Rt△ACO中,有OC=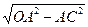 .
.
又∵A点坐标(5,0), AC=3,
∴OC=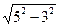 =4.
=4.
∴tan∠OAC=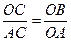 .
.
∴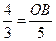 .解得 OB=
.解得 OB=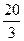 .
.
又∵D为OB中点,∴OD=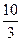 .
.
D点坐标为(0,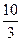 ).………………………(5分)
).………………………(5分)
连接AD,设直线AD的解析式为y=kx+b,则有
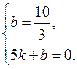 j解得
j解得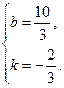
∴直线AD为y=-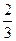 x+
x+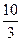 .
.
∵二次函数的图象过M(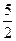 ,0)、A(5,0),
,0)、A(5,0),
∴抛物线对称轴x=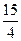 .………………………(6分)
.………………………(6分)
∵点M、A关于直线x=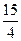 对称,设直线AD与直线x=
对称,设直线AD与直线x=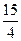 交于点P,
交于点P,
∴PD+PM为最小.
又∵DM为定长,
∴满足条件的点P为直线AD与直线x=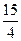 的交点.………………………(7分)
的交点.………………………(7分)
当x=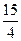 时,y=-
时,y=-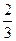
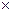
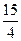 +
+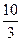 =
=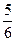 .
.
故P点的坐标为(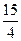 ,
,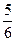 ).………………………(8分)
).………………………(8分)
(3)解:存在.
∵S△PDM=S△DAM-S△PAM
=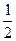 AM·yD-
AM·yD-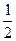 AM·yP
AM·yP
=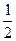 AM(yD-yp).
AM(yD-yp).
S△QAM=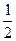 AM·
AM·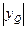 ,由(2)知D(0,
,由(2)知D(0,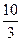 ),P(
),P(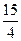 ,
,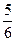 ),
),
∴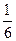 ×(
×(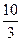 -
-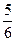 )=yQ 解得yQ=±
)=yQ 解得yQ=±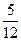 ………………………(9分)
………………………(9分)
∵二次函数的图像过M(0,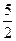 )、A(5,0),
)、A(5,0),
∴设二次函数解析式为y=a(x-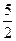 )(x-5).
)(x-5).
又∵该图象过点D(0,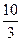 ),
),
a×(-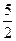 )×(-5)=
)×(-5)=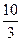 ,a=
,a=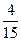 .
.
∴y=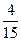 (x-
(x-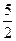 )(x-5).………………………(10分)
)(x-5).………………………(10分)
又∵C点在抛物线上,且yQ=±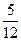 ,
,
∴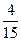 (x-
(x-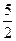 )(x-5)=±
)(x-5)=±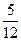 .
.
解之,得x1=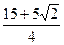 ,x2=
,x2=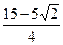 ,x3=
,x3=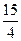 .
.
∴点Q的坐标为(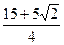 ,
,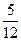 ),或(
),或(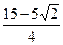 ,
,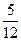 ),或(
),或(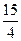 ,-
,-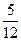 ).…………(12分)
).…………(12分)












