22.一只不透明的袋子中,装有分别标有数字1、2、3的三个球,这些除所外都相同,搅匀后从摸出个,记录下后放回袋并搅匀,再从任意摸出个,记录下,请用列表或画树状图方法,求出两次摸出上之和为偶数概率.
【答案】解:画树状图得:
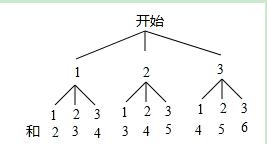
∵共有9种等可能的结果,两次摸出的球上的数字之和为偶数的有5种情况,
∴两次摸出的球上的数字之和为偶数的概率为: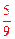 。
。
23. 如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB。
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形。
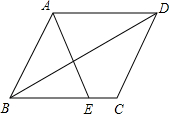
【答案】证明:(1)∵在平行四边形ABCD中,AD∥BC,∴∠AEB=∠EAD。
∵AE=AB,∴∠ABE=∠AEB。
∴∠ABE=∠EAD。
(2)∵AD∥BC,∴∠ADB=∠DBE。
∵∠ABE=∠AEB,∠AEB=2∠ADB,∴∠ABE=2∠ADB。
∴∠ABD=∠ABE-∠DBE=2∠ADB-∠ADB=∠ADB。∴AB=AD。
又∵四边形ABCD是平行四边形,∴四边形ABCD是菱形.。
24.实践操作:如图,△ABC是直角三角形,∠ACB=900,利用直尺和圆规按下列要求作图,并在图中表明相应的字母。(保留痕迹,不写作法)
(1)作BAC的平分线,交BC于点O;
(2)以O为圆心,OC为半径作圆。
综合运用:在你所作的图中,
(1)AB与⊙O的位置关系是_________ ;(直接写出答案)
(2)若AC=5,BC=12,求⊙O的半径。

【答案】解:实践操作:如图所示:
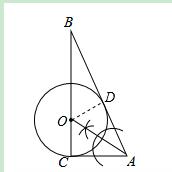
综合运用:
(1)相切。
(2)∵AC=5,BC=12,∴AD=5,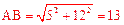 。
。
∴DB=13-5=7。
设半径为x,则OC=OD=x,BO=12-x,
∴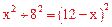 ,解得:
,解得: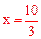 。
。
∴⊙O的半径为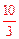 。
。
25.水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种80千克的钱,现在可买88千克。
(1)现在实际这种每千克多少元?
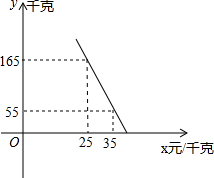
(2)准备这种,若这种的量y(千克)与单价x(元/千克)满足如图所示的一次函数关系。
①求y与x之间的函数关系式;
②请你帮拿个主意,将这种的单价定为多少时,能获得最大利润?最大利润是多少?(利润=收入-进货金额)
【答案】解:(1)设现在实际购进这种水果每千克x元,则原来购进这种水果每千克(x+2)元,由题意,得
80(x+2)=88x,解得x=20。
∴现在实际购进这种水果每千克20元。
(2)①设y与x之间的函数关系式为y=kx+b,
将(25,165),(35,55)代入,得
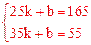 ,解得
,解得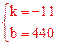 。
。
∴y与x之间的函数关系式为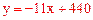 。
。
②设这种水果的销售单价为x元时,所获利润为w元,则
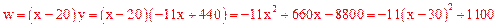 ,
,
∴当x=30时,w有最大值1100。
∴将这种水果的销售单价定为30元时,能获得最大利润,最大利润是1100元。












