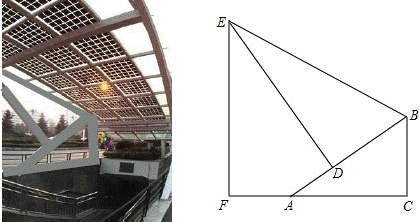
26.如图是某地下商业街的入口,数学课外兴趣小组同学打算运用所学知识测量侧面支架最高点E到地面距离EF.经测量,支架立柱BC与地面垂直,即∠BCA=90°,且BC=1.5cm,点F、A、C在同一条水平线上,斜杆AB与水平线AC夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架边BE与AB夹角∠EBD=60°,又测得AD=1m。请你求出该支架边BE及顶端E到地面距离EF长度。
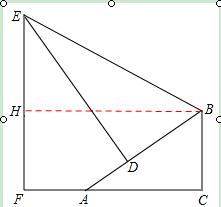
【答案】解:过B作BH⊥EF于点H,
∴四边形BCFH为矩形,BC=HF=1.5m,∠HBA=∠AC=30°。
在Rt△ABC中,∵∠BAC=30°,BC=1.5m,∴AB=3m。
∵AD=1m,∴BD=2m。
在Rt△EDB中,∵∠EBD=60°,∴∠BED=90°-60°=30°。
∴EB=2BD=2×2=4m。
又∵∠HBA=∠BAC=30°,∴∠EBH=∠EBD--∠HBD=30°,
∴EH=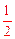 EB=2m。
EB=2m。
∴EF=EH+HF=2+1.5=3.5(m)。
答:该支架的边BE为4m,顶端E到地面的距离EF的长度为3.5m.
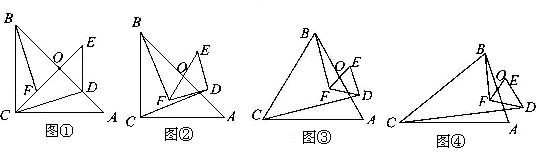
27. 阅读材料:如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=900,且点D 在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD。
解决问题:
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中结论仍然成立吗?如果成立,请说明理由;如果不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为O,且顶角∠ACB=∠EDF=α,请直接写出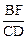 的值(用含α的式子表示出来)。
的值(用含α的式子表示出来)。
【答案】解:(1)相等。证明如下:
如图,连接CO、DO,
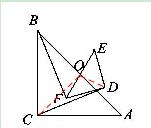
∵△ABC是等腰直角三角形,点O是AB的中点,
∴BO=CO,CO⊥AB。∴∠BOC=900。
同理,FO=DO,∠DOF=900。
∴∠BOF=900+∠COF,∠COD=900+∠COF。
∴∠BOF=∠COD。∴△BOF≌△COD(SAS)。
∴BF=CD。
(2)不成立。
如图,连接CO、DO,
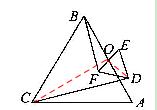
∵△ABC是等边三角形,∴∠CBO=600。
∵点O是AB的中点,∴CO⊥AB,即∠BOC=900。
∴在Rt△BOC中,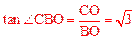 。
。
同理,∠DOF=900,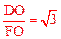 。∴
。∴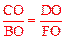 。
。
又∵∠BOF=900+∠COF,∠COD=900+∠COF。
∴∠BOF=∠COD。∴△BOF∽△COD。∴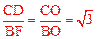 。
。
∴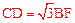 。
。
(3)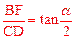 。
。
28.如图①,若二次函数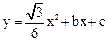 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数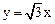 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
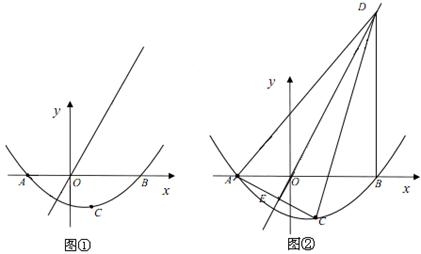
(3)如图②,过点B作DB⊥x轴交正比例函数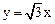 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数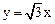 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
【答案】解:(1)∵二次函数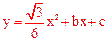 的图象与x轴交于点A(-2,0),B(3,0)两点,
的图象与x轴交于点A(-2,0),B(3,0)两点,
∴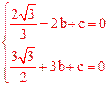 ,解得
,解得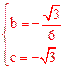 。
。
∴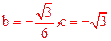 。
。
(2)证明:由(1)得二次函数解析式为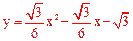 。
。
在正比例函数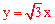 的图象上取一点F
的图象上取一点F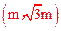 ,作FH⊥x轴于点H,则
,作FH⊥x轴于点H,则
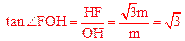 。∴
。∴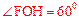 。
。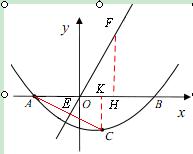
连接AC交 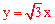 的图象于点E,作CK x轴于点K,
的图象于点E,作CK x轴于点K,
∵点A关于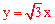 的图象的对称点为C,
的图象的对称点为C,
∴OE垂直平分AC。
∵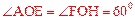 ,OA=2,
,OA=2,
∴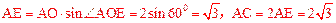 。
。
在Rt△ACK中,∵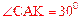 ,
,
∴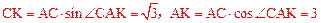 。∴
。∴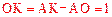 。
。
∴点C 的坐标为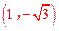 。
。
将C 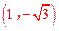 代入
代入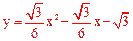 ,左边=右边,
,左边=右边,
∴点C在所求的二次函数的图象上。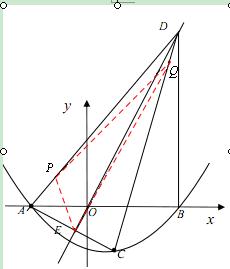
(3)∵DB⊥x轴交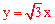 的图象于点D,B(3,0),
的图象于点D,B(3,0),
∴把x=3代入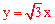 得
得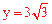 ,即BD=
,即BD=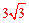 。
。
在Rt△ACK中,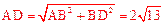 ,
,
∵OE垂直平分AC,
∴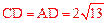 ,
,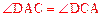 。
。
假设存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,
则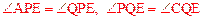 。
。
∵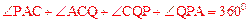 , ∴
, ∴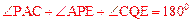 。
。
又∵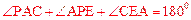 ,∴
,∴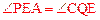 。
。
又∵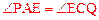 ,∴△PAE∽△ECQ。∴
,∴△PAE∽△ECQ。∴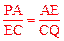 ,即
,即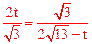 。
。
整理,得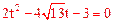 ,解得
,解得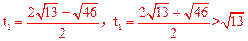 (不合题意,舍去)。
(不合题意,舍去)。
∴存在时刻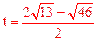 ,使PE平分∠APQ,同时QE平分∠PQC。
,使PE平分∠APQ,同时QE平分∠PQC。












