一. 选择题:本小题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 函数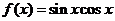 最小值是
最小值是
A.-1 B. 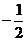 C.
C. 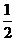 D.1
D.1
1.【答案】:B
[解析]∵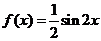 ∴
∴ .故选B
.故选B
2.已知全集U=R,集合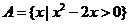 ,则
,则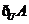 等于
等于
A. { x ∣0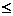 x
x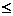 2} B { x ∣0<x<2}
2} B { x ∣0<x<2}
C. { x ∣x<0或x>2} D { x ∣x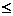 0或x
0或x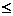 2}
2}
2.【答案】:A
[解析]∵计算可得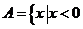 或
或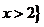 ∴
∴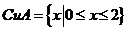 .故选A
.故选A
3.等差数列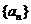 的前n项和为
的前n项和为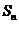 ,且
,且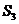 =6,
=6,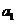 =4, 则公差d等于
=4, 则公差d等于
A.1 B 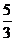 C.- 2 D 3
C.- 2 D 3
3.【答案】:C
[解析]∵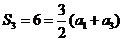 且
且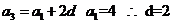 .故选C
.故选C
4. 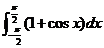 等于
等于
A.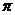 B. 2 C.
B. 2 C. 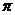 -2 D.
-2 D. 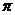 +2
+2
4.【答案】:D
[解析]∵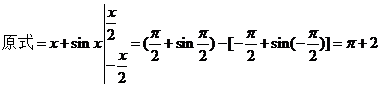 .故选D
.故选D
5.下列函数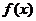 中,满足“对任意
中,满足“对任意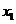 ,
,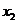
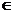 (0,
(0,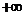 ),当
),当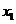 <
<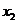 时,都有
时,都有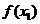 >
>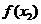 的是
的是
A.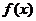 =
= B.
B. 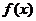 =
=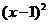 C .
C .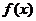 =
=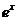 D
D 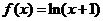
5.【答案】:A
[解析]依题意可得函数应在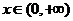 上单调递减,故由选项可得A正确。
上单调递减,故由选项可得A正确。
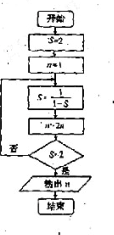
6.阅读右图所示的程序框图,运行相应的程序,输出的结果是
A.2 B .4 C. 8 D .16
6.【答案】:C
[解析]由算法程序图可知,在n =4前均执行”否”命令,故n=2×4=8. 故选C
7.设m,n是平面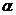 内的两条不同直线,
内的两条不同直线,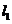 ,
,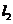 是平面
是平面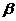 内的两条相交直线,则
内的两条相交直线,则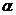 //
// 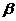 的一个充分而不必要条件是
的一个充分而不必要条件是

A.m // 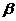 且l //
且l // 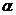 B. m // l 且n // l
B. m // l 且n // l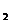
C. m // 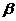 且n //
且n // 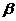 D. m //
D. m // 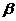 且n // l
且n // l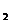
7.【答案】:B
[解析]若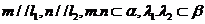 ,则可得
,则可得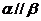 .若
.若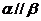 则存在
则存在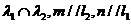
8.已知某运动员每次投篮命中的概率都为40%。现采用随机模拟的方法估计该运动
员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,
指定1,2,3,4表示命中,5,6,,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果。经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为
A.0.35 B 0.25 C 0.20 D 0.15
8.【答案】:B
[解析]由随机数可估算出每次投篮命中的概率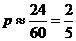 则三次投篮命中两次为
则三次投篮命中两次为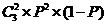
 0.25故选B
0.25故选B
9.设a,b,c为同一平面内具有相同起点的任意三个非零向量,且满足a与b不共线,
a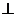 c ∣a∣=∣c∣,则∣b • c∣的值一定等于
c ∣a∣=∣c∣,则∣b • c∣的值一定等于

A. 以a,b为两边的三角形面积 B 以b,c为两边的三角形面积
C.以a,b为邻边的平行四边形的面积 D 以b,c为邻边的平行四边形的面积
9.【答案】:C
[解析]依题意可得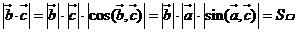 故选C.
故选C.
10.函数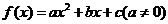 的图象关于直线
的图象关于直线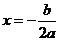 对称。据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程
对称。据此可推测,对任意的非零实数a,b,c,m,n,p,关于x的方程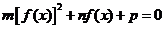 的解集都不可能是
的解集都不可能是
A. 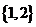 B
B 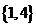 C
C 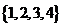 D
D 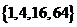
10. 【答案】:D
[解析]本题用特例法解决简洁快速,对方程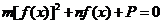 中
中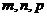 分别赋值求出
分别赋值求出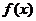 代入
代入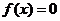 求出检验即得.
求出检验即得.