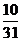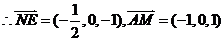第二卷 (非选择题共100分)
二、填空题:本大题共5小题,每小题4分,共20分。把答案填在答题卡的相应位置。
11.若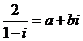 (i为虚数单位,
(i为虚数单位,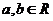 )则
)则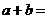 _________
_________ 

11. 【答案】:2
解析:由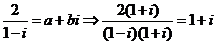 ,所以
,所以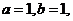 故
故 。
。
12.某校开展“爱我海西、爱我家乡”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示。记分员在去掉一个最高分和一个最低分后,算的平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清。若记分员计算无误,则数字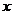 应该是___________
应该是___________

12. 【答案】:1
解析:观察茎叶图,
可知有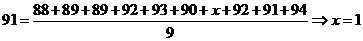 。
。
13.过抛物线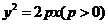 的焦点F作倾斜角为
的焦点F作倾斜角为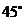 的直线交抛物线于A、B两点,若线段AB的长为8,则
的直线交抛物线于A、B两点,若线段AB的长为8,则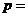 ________________
________________ 

13. 【答案】:2
解析:由题意可知过焦点的直线方程为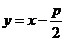 ,联立有
,联立有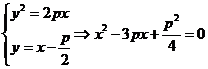 ,又
,又 。
。
14.若曲线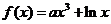 存在垂直于
存在垂直于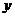 轴的切线,则实数
轴的切线,则实数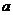 取值范围是_____________.
取值范围是_____________.
14. 【答案】: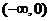
解析:由题意可知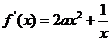 ,又因为存在垂直于
,又因为存在垂直于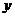 轴的切线,
轴的切线,
所以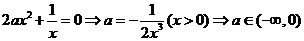 。
。
15.五位同学围成一圈依序循环报数,规定:
①第一位同学首次报出的数为1,第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;
②若报出的数为3的倍数,则报该数的同学需拍手一次
已知甲同学第一个报数,当五位同学依序循环报到第100个数时,甲同学拍手的总次数为________.
15. 【答案】:5
解析:由题意可设第 次报数,第
次报数,第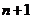 次报数,第
次报数,第 次报数分别为
次报数分别为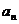 ,
,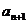 ,
, ,所以有
,所以有 ,又
,又 由此可得在报到第100个数时,甲同学拍手5次。
由此可得在报到第100个数时,甲同学拍手5次。
三、解答题

16.(13分)
从集合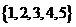 的所有非空子集中,等可能地取出一个。
的所有非空子集中,等可能地取出一个。
(1) 记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;
(2) 记所取出的非空子集的元素个数为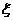 ,求
,求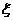 的分布列和数学期望E
的分布列和数学期望E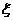
16、解:(1)记”所取出的非空子集满足性质r”为事件A
基本事件总数n=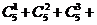
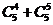 =31
=31
事件A包含的基本事件是{1,4,5}、{2,3,5}、{1,2,3,4}
事件A包含的基本事件数m=3
所以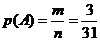
(II)依题意,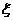 的所有可能取值为1,2,3,4,5
的所有可能取值为1,2,3,4,5
又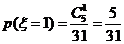 ,
, 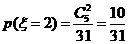 ,
, 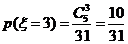
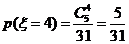 ,
, 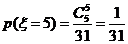
故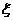 的分布列为:
的分布列为:
| 1 | 2 | 3 | 4 | 5 |
P | |
| | | |
从而E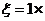
 +2
+2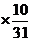 +3
+3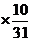 +4
+4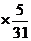 +5
+5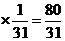
17(13分)
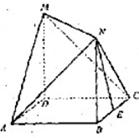
如图,四边形ABCD是边长为1的正方形,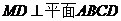 ,
,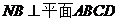 ,且MD=NB=1,E为BC的中点
,且MD=NB=1,E为BC的中点
(1)求异面直线NE与AM所成角的余弦值
(2)在线段AN上是否存在点S,使得ES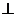 平面AMN?若存在,求线段AS的长;若不存在,请说明理由
平面AMN?若存在,求线段AS的长;若不存在,请说明理由

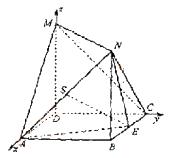
17.解析:(1)在如图,以D为坐标原点,建立空间直角坐标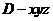 依题意,得
依题意,得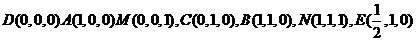 。
。
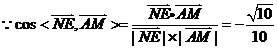 ,
,
所以异面直线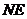 与
与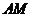 所成角的余弦值为
所成角的余弦值为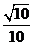 .A
.A
(2)假设在线段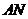 上存在点
上存在点 ,使得
,使得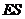
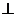 平面
平面 .
.
 ,
,
可设
又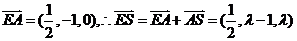 .
.
由 平面
平面 ,得
,得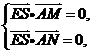 即
即
故 ,此时
,此时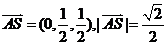 .
.
经检验,当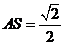 时,
时, 平面
平面 .
.
故线段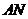 上存在点
上存在点 ,使得
,使得 平面
平面 ,此时
,此时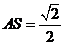 .
.
18、(本小题满分13分)
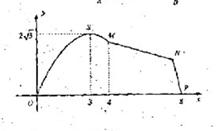
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数
y=Asin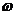 x(A>0,
x(A>0, 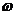 >0) x
>0) x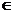 [0,4]的图象,且图象的最高点为S(3,2
[0,4]的图象,且图象的最高点为S(3,2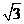 );赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定
);赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定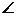 MNP=120
MNP=120
(I)求A , 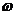 的值和M,P两点间的距离;
的值和M,P两点间的距离;
(II)应如何设计,才能使折线段赛道MNP最长? 

18.本小题主要考查三角函数的图象与性质、解三角形等基础知识,考查运算求解能力以及应用数学知识分析和解决实际问题的能力,考查化归与转化思想、数形结合思想,
解法一
(Ⅰ)依题意,有 ,
, ,又
,又 ,
,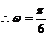 。
。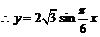
当 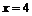 是,
是,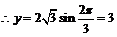
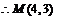 又
又
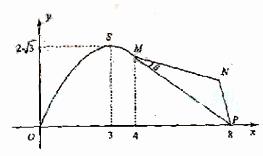
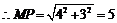
(Ⅱ)在△MNP中∠MNP=120°,MP=5,
设∠PMN=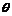 ,则0°<
,则0°<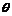 <60°
<60°
由正弦定理得
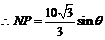 ,
,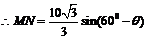
故
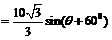
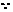 0°<
0°<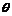 <60°,
<60°, 当
当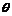 =30°时,折线段赛道MNP最长
=30°时,折线段赛道MNP最长
亦即,将∠PMN设计为30°时,折线段道MNP最长
解法二:
(Ⅰ)同解法一
(Ⅱ)在△MNP中,∠MNP=120°,MP=5,
由余弦定理得 ∠MNP=
∠MNP=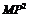
即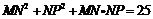
故
从而 ,即
,即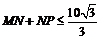
当且仅当 时,折线段道MNP最长
时,折线段道MNP最长
注:本题第(Ⅱ)问答案及其呈现方式均不唯一,除了解法一、解法二给出的两种设计方式,还可以设计为:① ;②
;② ;③点N在线段MP的垂直平分线上等
;③点N在线段MP的垂直平分线上等