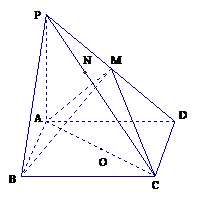
20.(本小题满分12分)
在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面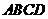 ,
,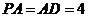 ,
,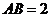 . 以
. 以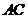 的中点
的中点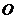 为球心、
为球心、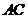 为直径的球面交
为直径的球面交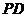 于点
于点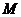 ,交
,交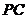 于点
于点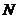 .
.
(1)求证:平面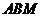 ⊥平面
⊥平面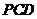 ;
; 
(2)求直线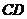 与平面
与平面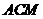 所成的角的大小;
所成的角的大小;
(3)求点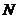 到平面
到平面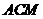 的距离.
的距离.
解:
方法一:(1)依题设知,AC是所作球面的直径,则AM⊥MC。
又因为P A⊥平面ABCD,则PA⊥CD,又CD⊥AD,
所以CD⊥平面PAD,则CD⊥AM,所以A M⊥平面PCD,
所以平面ABM⊥平面PCD。
(2)由(1)知,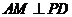 ,又
,又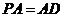 ,则
,则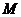 是
是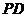 的中点可得
的中点可得
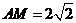 ,
,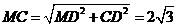
则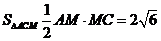
设D到平面ACM的距离为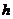 ,由
,由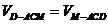 即
即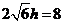 ,
,
可求得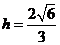 ,
,
设所求角为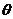 ,则
,则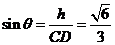 ,
,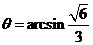 。
。
(3) 可求得PC=6。因为AN⊥NC,由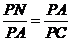 ,得PN
,得PN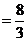 。所以
。所以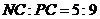 。
。
故N点到平面ACM的距离等于P点到平面ACM距离的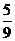 。
。
又因为M是PD的中点,则P、D到平面ACM的距离相等,由(2)可知所求距离为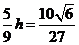 。
。
方法二:
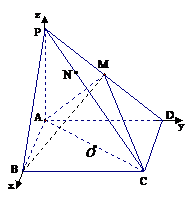
(1)同方法一;
(2)如图所示,建立空间直角坐标系,则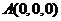 ,
,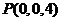 ,
,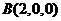 ,
, 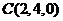 ,
,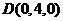 ,
,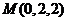 ;设平面
;设平面 的一个法向量
的一个法向量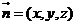 ,由
,由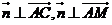 可得:
可得: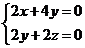 ,令
,令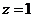 ,则
,则
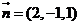 。设所求角为
。设所求角为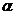 ,则
,则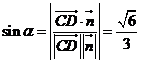 ,
,
所以所求角的大小为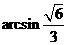 。
。
(3)由条件可得,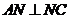 .在
.在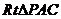 中,
中,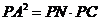 ,所以
,所以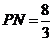 ,则
,则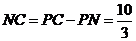 ,
, 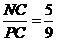 ,所以所求距离等于点
,所以所求距离等于点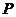 到平面
到平面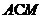 距离的
距离的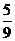 ,设点
,设点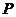 到平面
到平面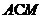 距离为
距离为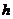 则
则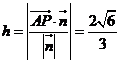 ,所以所求距离为
,所以所求距离为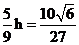 。
。
21.(本小题满分12分)
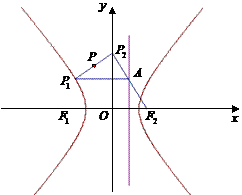
已知点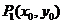 为双曲线
为双曲线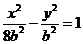 (
(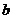 为正常数)上任一点,
为正常数)上任一点,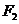 为双曲线的右焦点,过
为双曲线的右焦点,过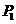 作右准线的垂线,垂足为
作右准线的垂线,垂足为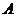 ,连接
,连接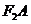 并延长交
并延长交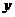 轴于
轴于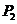 .
.
(1) 求线段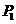
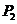 的中点
的中点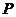 的轨迹
的轨迹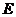 的方程;
的方程;
(2) 设轨迹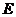 与
与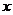 轴交于
轴交于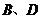 两点,在
两点,在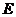 上任取一点
上任取一点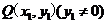 ,直线
,直线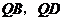 分别交
分别交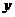 轴于
轴于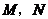 两点.求证:以
两点.求证:以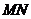 为直径的圆过两定点.
为直径的圆过两定点.
解: (1) 由已知得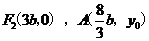 ,则直线
,则直线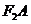 的方程为:
的方程为: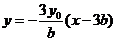 ,
,
令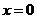 得
得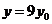 ,即
,即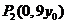 ,
,
设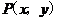 ,则
,则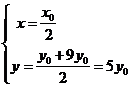 ,即
,即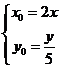 代入
代入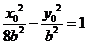 得:
得: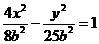 ,
,
即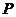 的轨迹
的轨迹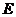 的方程为
的方程为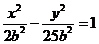 .
.
(2) 在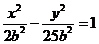 中令
中令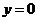 得
得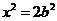 ,则不妨设
,则不妨设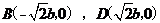 ,
,
于是直线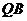 的方程为:
的方程为: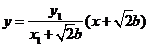 ,
, 直线
直线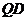 的方程为:
的方程为: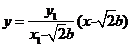 ,
,
则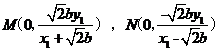 ,
,
则以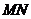 为直径的圆的方程为:
为直径的圆的方程为: 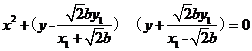
 ,
,
令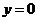 得:
得: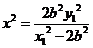 ,而
,而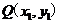 在
在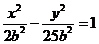 上,则
上,则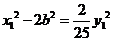 ,
,
于是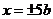 ,即以
,即以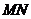 为直径的圆过两定点
为直径的圆过两定点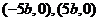 .
.
22.(本小题满分14分)
各项均为正数的数列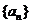 ,
,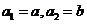 ,且对满足
,且对满足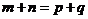 的正整数
的正整数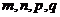 都有
都有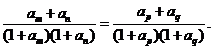
(1)当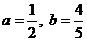 时,求通项
时,求通项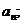
(2)证明:对任意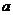 ,存在与
,存在与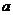 有关的常数
有关的常数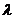 ,使得对于每个正整数
,使得对于每个正整数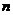 ,都有
,都有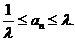
解:(1)由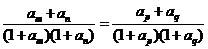 得
得
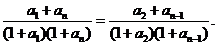 将
将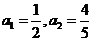 代入化简得
代入化简得
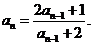
所以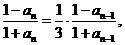
故数列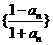 为等比数列,从而
为等比数列,从而
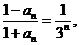 即
即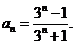
可验证,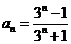 满足题设条件.
满足题设条件.
(2) 由题设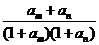 的值仅与
的值仅与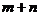 有关,记为
有关,记为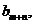 则
则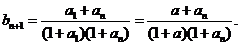
考察函数 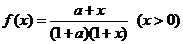 ,则在定义域上有
,则在定义域上有
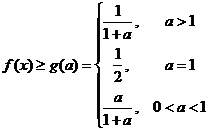
故对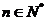 ,
, 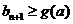 恒成立.
恒成立.
又 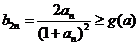 ,
,
注意到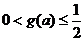 ,解上式得
,解上式得
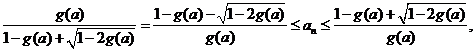
取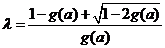 ,即有
,即有 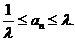 .
.