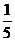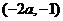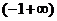21.本小题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力、考查函数与方程思想、数形结合思想、化归与转化思想、分类与整合思想,满分12分。
解法一:
(I)依题意,得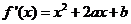
由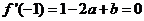 得
得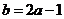
(Ⅱ)由(I)得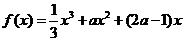 (
(
故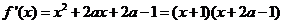
令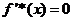 ,则
,则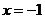 或
或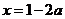
①当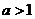 时,
时,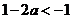
当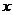 变化时,
变化时,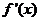 与
与 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| + | — | + |
| 单调递增 | 单调递减 | 单调递增 |
由此得,函数 的单调增区间为
的单调增区间为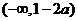 和
和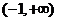 ,单调减区间为
,单调减区间为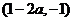
②由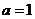 时,
时,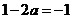 ,此时,
,此时,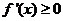 恒成立,且仅在
恒成立,且仅在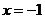 处
处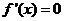 ,故函数
,故函数 的单调区间为R
的单调区间为R
③当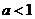 时,
时,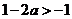 ,同理可得函数
,同理可得函数 的单调增区间为
的单调增区间为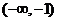 和
和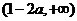 ,单调减区间为
,单调减区间为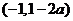
综上:
当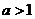 时,函数
时,函数 的单调增区间为
的单调增区间为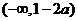 和
和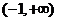 ,单调减区间为
,单调减区间为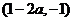 ;
;
当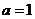 时,函数
时,函数 的单调增区间为R;
的单调增区间为R;
当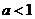 时,函数
时,函数 的单调增区间为
的单调增区间为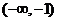 和
和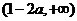 ,单调减区间为
,单调减区间为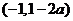
(Ⅲ)当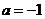 时,得
时,得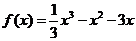
由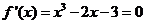 ,得
,得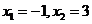
由(Ⅱ)得 的单调增区间为
的单调增区间为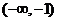 和
和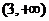 ,单调减区间为
,单调减区间为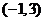
所以函数 在
在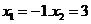 处取得极值。
处取得极值。
故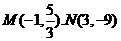
所以直线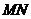 的方程为
的方程为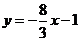
由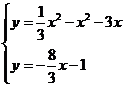 得
得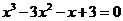
令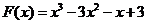
易得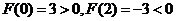 ,而
,而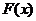 的图像在
的图像在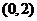 内是一条连续不断的曲线,
内是一条连续不断的曲线,
故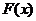 在
在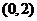 内存在零点
内存在零点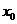 ,这表明线段
,这表明线段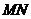 与曲线
与曲线 有异于
有异于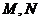 的公共点
的公共点
解法二:
(I)同解法一
(Ⅱ)同解法一。
(Ⅲ)当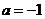 时,得
时,得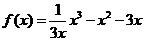 ,由
,由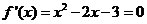 ,得
,得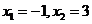
由(Ⅱ)得 的单调增区间为
的单调增区间为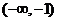 和
和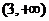 ,单调减区间为
,单调减区间为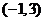 ,所以函数
,所以函数 在
在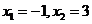 处取得极值,
处取得极值,
故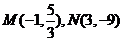
所以直线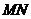 的方程为
的方程为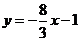
由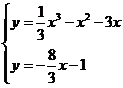 得
得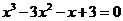
解得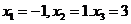
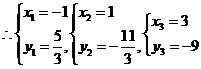
所以线段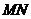 与曲线
与曲线 有异于
有异于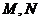 的公共点
的公共点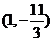
22.本小题主要考查直线、椭圆、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,满分14分
解法一:
(I)由已知得,椭圆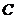 的左顶点为
的左顶点为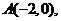 上顶点为
上顶点为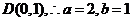
故椭圆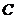 的方程为
的方程为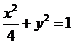
(Ⅱ)直线AS的斜率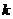 显然存在,且
显然存在,且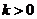 ,故可设直线
,故可设直线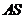 的方程为
的方程为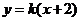 ,从而
,从而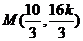
由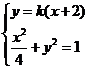 得
得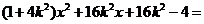 0
0
设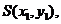 则
则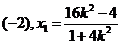 得
得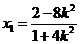 ,从而
,从而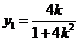
即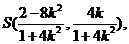 又
又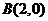
由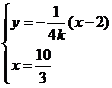 得
得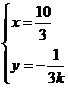
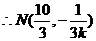
故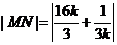
又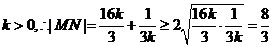
当且仅当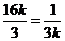 ,即
,即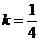 时等号成立
时等号成立
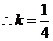 时,线段
时,线段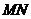 的长度取最小值
的长度取最小值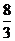
(Ⅲ)由(Ⅱ)可知,当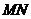 取最小值时,
取最小值时,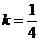
此时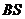 的方程为
的方程为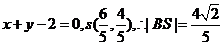
要使椭圆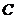 上存在点
上存在点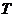 ,使得
,使得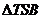 的面积等于
的面积等于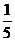 ,只须
,只须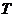 到直线
到直线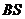 的距离等于
的距离等于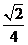 ,所以
,所以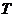 在平行于
在平行于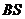 且与
且与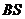 距离等于
距离等于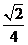 的直线
的直线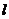 上。
上。
设直线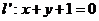
则由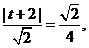 解得
解得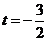 或
或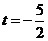
① 当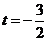 由
由 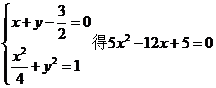
由于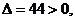 故直线
故直线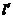 与椭圆C有两个不同的交点
与椭圆C有两个不同的交点
② 当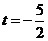 由
由 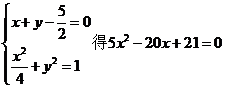
由于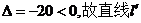 与椭圆C没有交点
与椭圆C没有交点
综上所述,当线段MN的长度最小时,椭圆上仅存在两个不同的点T,使得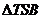 的面积等于
的面积等于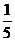
解法二:
(Ⅰ)同解法一
(Ⅱ)设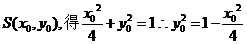
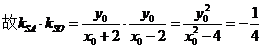
设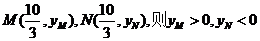
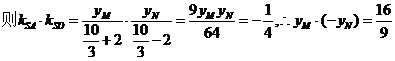
故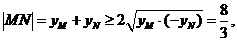
当且仅当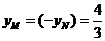 时等号成立
时等号成立
即M,N的长度的最小值为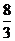
(Ⅲ)由(Ⅱ)知,当M,N取最小值时,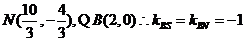
此时BS的方程为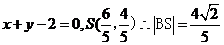
设与直线BS平行的直线方程为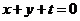
由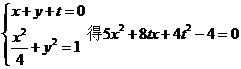
当直线与椭圆C有唯一公共点时,有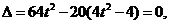 解得
解得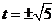
当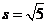 时,两平行直线BS:
时,两平行直线BS: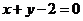 与
与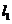 :
: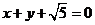 间的距离
间的距离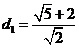 ,
,
当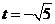 时,两平行直线BS:
时,两平行直线BS: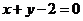 与
与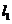 :
: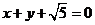 间的距离
间的距离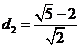 ,
,
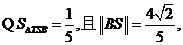 故
故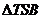 在BS边上的高
在BS边上的高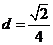
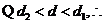 椭圆C上存在两个不同的点T,使得
椭圆C上存在两个不同的点T,使得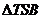 的面积等于
的面积等于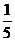
即线段MN的长度最小时,椭圆C上仅存在两个不同的点T,使得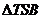 的面积等于
的面积等于