评论
打印
选择题部分（共50分）
一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1、设集合S={x|x>-2},T={x|-4≤x≤1},则S∩T=
A、[-4,+∞） B、（-2, +∞） C、[-4,1] D、(-2,1]
【答案】D
【解析】如图1所示
，所以选D
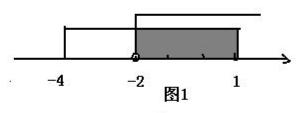
【考点定位】此题考查集合的运算，利用数轴即可解决此题，体现数形结合思想的应用，此考点是历年来高考必考考点之一，属于简单题。
2、已知i是虚数单位，则(2+i)(3+i)=
A、5-5i B、7-5i C、5+5i D、7+5i
【答案】C
【解析】原始=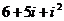
=6+5i-1=5+5i,所以选C
【考点定位】此题考查复数的乘法运算，考查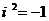
这个只是点，属于简单题。
3、若αR，则“α=0”是“sinα<cosα”的
A、充分不必要条件 B、必要不充分条件
C、充分必要条件 D、既不充分也不必要条件
【答案】A
【解析】此题中，由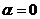
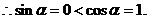，所以是充分条件，反之
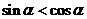，得出
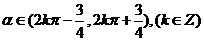即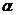
不一定等于0，所以是不必要条件选A
【考点定位】此题考查充分条件判断和三角函数的知识点；充分和必要条件判断的三种方法
4、设m、n是两条不同的直线，α、β是两个不同的平面，
A、若m∥α，n∥α,则m∥n B、若m∥α，m∥β,则α∥β
C、若m∥n，m⊥α,则n⊥α D、若m∥α，α⊥β,则m⊥β
【答案】C
【解析】
【考点定位】此题考查线线、线面、面面平行与垂直的判定定理和性质定理
5、已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是
A、108cm3 B、100 cm3 C、92cm3 D、84cm3
【答案】B
【解析】
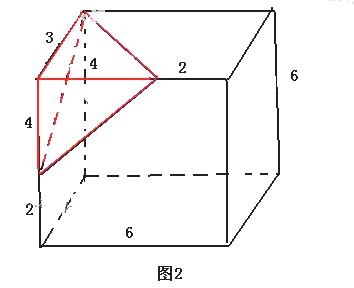
【考点定位】此题考查三视图知识，多面体的体积计算公式。
6、函数f(x)=sin xcos x+cos 2x的最小正周期和振幅分别是
A、π，1 B、π，2 C、2π，1 D、2π，2
【答案】A
【解析】此题原式=
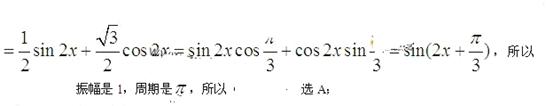
【考点定位】此题考查二倍角正弦公式、两角和与差正余弦公式的灵活应用，考查
7、已知a、b、cR，函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1)，则
A、a>0,4a+b=0 B、a<0,4a+b=0
C、a>0,2a+b=0 D、a<0,2a+b=0
【答案】A
【解析】由f(0)=f(4)知，函数的对称轴是X=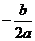
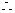b+4a=0 由f（0）>f（1）知函数在对称轴的左边递减，所以开口向上；所以选A
【考点定位】此题考查二次函数的性质，二次函数的开口有二次项系数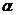决定，开口向上在对称轴左边递减，在对称轴右边递增；开口向下在对称轴左边递增，在对称轴右边递减
8、已知函数y=f(x)的图像是下列四个图像之一，且其导函数y=f’(x)的
图像如右图所示，则该函数的图像是
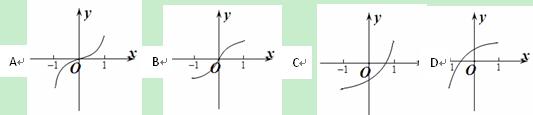
【答案】B
【解析】由导函数图像可知函数的函数值在[-1,1]上大于零，所以原函数递增，且导函数值在[-1,0]递增，即原函数在[-1,1]上切线的斜率递增，导函数的函数值在[0,1]递减，即原函数在[0,1]上切线的斜率递减，所以选B
【考点定位】此题考查导数的应用，考查利用导数的图像判断原函数的图像
9、如图F1、F2是椭圆C1：+y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是
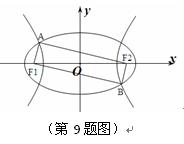
A、 B、 C、 D、
【答案】D
【解析】由已知得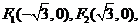
设双曲线实半轴为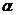，由椭圆及双曲线的定义和已知得到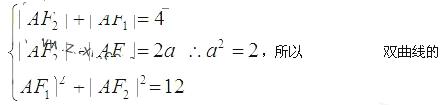
离心率为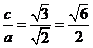
，所以选D
【考点定位】此题考查椭圆和双曲线的定义、性质的应用；
10、设a，bR，定义运算“∧”和“∨”如下：
 |  |
a∧b= a∨b=
若正数a、b、c、d满足ab≥4,c+d≤4,则
A、a∧b≥2,c∧d≤2 B、a∧b≥2,c∨d≥2
C、a∨b≥2,c∧d≤2 D、a∨b≥2,c∨d≥2
【答案】C
【解析】
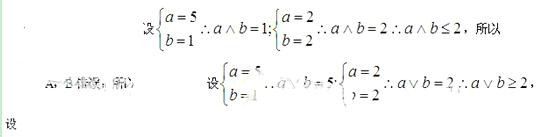
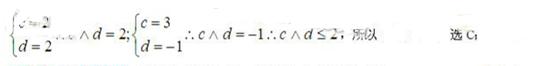
【考点定位】此题是信息类的题目，考查学生的自学能力和逻辑推理能力；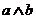
的意思是取两个量中的较小的，
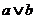的意思是取两个量中的较大的，采用特殊值法
