选择题部分(共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设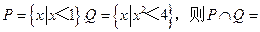
(A)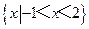 (B)
(B)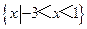
(C)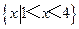 (D)
(D)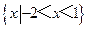
答案D
【命题意图】本题考查集合运算,需先求出集合Q的具体的范围,然后求交集.
【解析】由题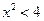 ,所以
,所以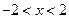 ,所以
,所以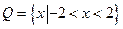 ,所以
,所以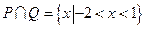 ,故选D.
,故选D.
(2)已知函数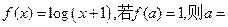
(A)0(B)1(C)2(D)3
答案B
【命题意图】本题主要考查对数的基本运算,直接利用已知条件中的等量关系求解.
【解析】由题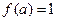 ,得到
,得到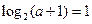 ,解得
,解得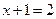 ,所以
,所以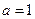 ,故选B.
,故选B.
(3)设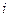 为虚数单位,则
为虚数单位,则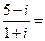
(A)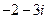 (B)
(B)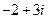 (C)
(C)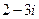 (D)
(D)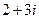
答案C
【命题意图】本题主要考查复数的基本运算,属于容易题.
【解析】由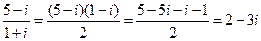 ,故选C.
,故选C.
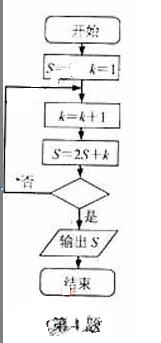
(4)某程度框图如图所示,若输出的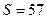 ,则判断框内为
,则判断框内为
(A)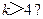 (B)
(B)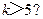
(C)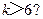 (D)
(D)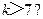
答案A
【命题意图】本题考查程序框图的有关知识,同时考查识图、用图能力.
【解析】由题开始k=k+1=1+1=2,s=2×1+2=4,不满足条件需继续循环,则k=k+1=2+1=3,s=2×4+3=11,k=k+1=3+1=4,s=2×11+4=26,k=k+1=4+1=5,s=2×26+5=57,此时满足条件,应输出S,所以判断框内应为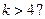 ,故选A.
,故选A.
(5) 设
设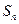 为等比数列
为等比数列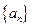 的前n项和,
的前n项和,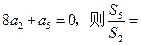
(A)-11(B)-8(C)5(D)11
(A)-11(B)-8(C)5(D)11
答案A
【命题意图】本题考查等比数列的基本运算.
【解析】由题数列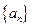 为等比数列,
为等比数列,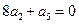 ,即
,即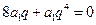 ,因为
,因为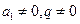 ,所以有
,所以有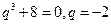 ,
,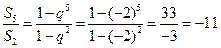 ,故选A.
,故选A.
(6)设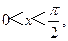 则“xsin2 x<1”是“xsin x<1”的
则“xsin2 x<1”是“xsin x<1”的
(A)充分而不必要条件(B)必要而不充分条件
(C)充分必要条件(D)既不充分也不必要条件
答案B
【命题意图】本题主要考查充要条件的判断.
【解析】因为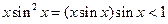 ,
,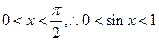 ,不一定能推出
,不一定能推出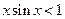 成立,但当
成立,但当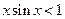 成立时,因为
成立时,因为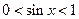 ,所以有
,所以有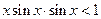 ,即
,即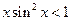 ,一定成立.故选
,一定成立.故选 B.
B.
(7)若实数x、y满足不等式组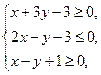 则x+y的最大值为
则x+y的最大值为
(A)9(B)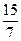
(C)1 (D)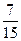
答案A
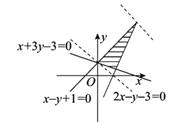
【命题意图】本题考查线性规划的有关最值问题,利用已知条件画出可行域求解.
【解析】已知约束条件形成的可行域如图所示当目标函数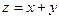 过
过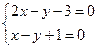 的交点
的交点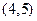 点时取得最大值为9,故选A.
点时取得最大值为9,故选A.
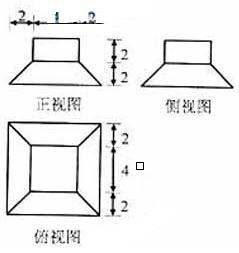
(8)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是
(A)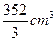 (B)
(B)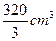
(C)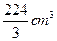 (D)
(D)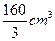
答案B
【命题意图】本题主要考查空间几何体的三视图及利用三视图求解几何体的体积等知 识.
识.
【解析】由三视图可知,该几何体是由一个正四棱柱和一个正四棱台组合形成的,由图中数据可知四棱柱的体积为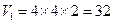 ,
,
底层正四棱台的体积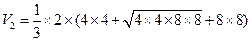
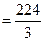 ,所以该组合体的体积为
,所以该组合体的体积为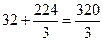 ,故选B.
,故选B.
(9)已知x0是函数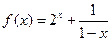 的一个零点,若
的一个零点,若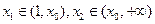 ,则
,则
(A)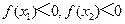 (B)
(B)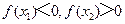
(C)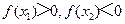 (D)
(D)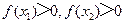
9.答案B
【命题意图】本题主要考查函数的零点问题及函数的单调性的判断.
【解析】由题可知已知函数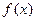 是由函数
是由函数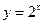 与
与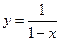 组合而成的,因为两个函数在
组合而成的,因为两个函数在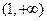 上均为增函数,所以
上均为增函数,所以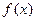 也是
也是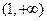 上的增函数,又因为
上的增函数,又因为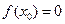 ,
,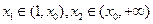 ,所以有函数的草图可知,
,所以有函数的草图可知,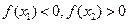 ,故选B.
,故选B.
(10)设O为坐标原点,F1,F2是双曲线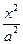 -
-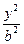 =1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1P F2=60°,
=1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1P F2=60°,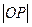 =
=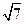 a,
a, 则该双曲线的渐近线方程为
则该双曲线的渐近线方程为
(A)x±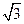 y=0(B)
y=0(B)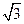 x±y=0
x±y=0
(C) x±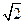 y=0(D)
y=0(D) 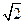 x±y=0
x±y=0
10.答案D
【命题意图】本题主要考查双曲线定义,余弦定理的应用,属于难题.
【解析】由题设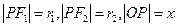 ,则由双曲线的定义可知
,则由双曲线的定义可知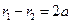 ①,在
①,在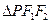 中由余弦定理可得
中由余弦定理可得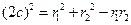 ,②
,②
在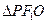 中,
中,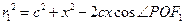 ,③
,③
在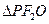 中,
中,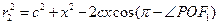 ④
④
由以上四式消掉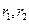 即可求出
即可求出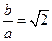 ,可知选D.
,可知选D.












