三.解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分l0分)(注意:在试题卷上作答无效)
设等比数列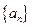 的前n项和为
的前n项和为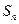 .已知
.已知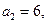
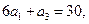 求
求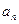 和
和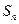 .
.
【思路点拨】解决本题的突破口是利用方程的思想建立关于a1和公比q的方程,求出a1和q,然后利用等比数列的通项公式及前n项和公式求解即可。
【解析】设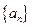 的公比为q,由题设得
的公比为q,由题设得
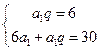 …………………………………3分
…………………………………3分
解得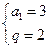 或
或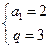 , …………………………………6分
, …………………………………6分
当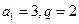 时,
时,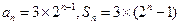 ;
;
当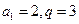 时,
时,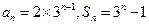 ……………………………10分
……………………………10分
(18)(本小题满分12分)(注意:在试题卷上作答无效)
△ABC的内角A、B、C的对边分别为a、b、c.己知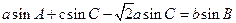 .
.
(Ⅰ)求B;
(Ⅱ)若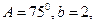
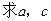 .
.
【思路点拨】第(I)问由正弦定理把正弦转化为边,然后再利用余弦定理即可解决。
(II)在(I)问的基础上知道两角一边可以直接利用正弦定理求解.
【解析】(I)由正弦定理得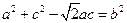 …………………………3分
…………………………3分
由余弦定理得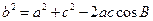 .
.
故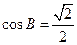 ,因此
,因此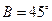 .…………………………………6分
.…………………………………6分
(II)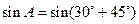
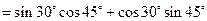
 …………………………………8分
…………………………………8分
故 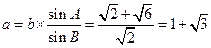
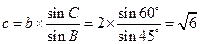 .…………………………………12分
.…………………………………12分
(19)(本小题满 分l2分)(注意:在试题卷上作答无效)
分l2分)(注意:在试题卷上作答无效)
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立.
(I)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(II)求该地3位车主中恰有1位车主甲、乙两种保险都不购买的概率.
【命题意图】本题主要考查独立事件的概率、对立事件的概率、互斥事件的概率及次独立重复试验发生k次的概率,考查考生分析问题、解决问题的能力.
【解析】记A表示事件:该地的1位车主购买甲种保险:
B表示事件:该地的1位车主购买乙种保险但不购买甲种保险。
C表示事件:该地的1位车主至少购买甲、乙两种保险中的1种;
D表示事件:该地的1位车主甲、乙两种保险都不购买;
E表示事件:该地的3位车主中恰有1位车主甲、乙两种保险都不购买.
(I)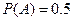 ,
, 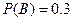 ,
, 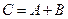 ……………………………3分
……………………………3分
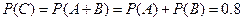 ……………………………6分
……………………………6分
(II)D=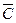 ,P(D)=1-P(C)=1-0.8=0.2, ……………………………9分
,P(D)=1-P(C)=1-0.8=0.2, ……………………………9分
P(E)=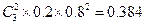 . ……………………………12分
. ……………………………12分
(20)(本小题满 分l2分)(注意:在试题卷上作答无效)
分l2分)(注意:在试题卷上作答无效)
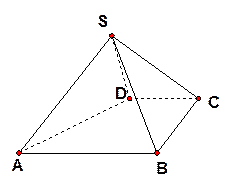
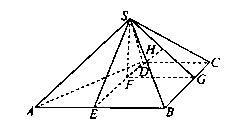
如图,四棱锥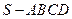 中,
中, 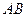 ∥
∥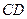 ,
,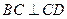 ,侧面
,侧面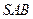 为等边三角形.
为等边三角形.
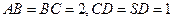 .
.
(I) 证明: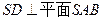
(II) 求AB与平面SBC所成角的大小。
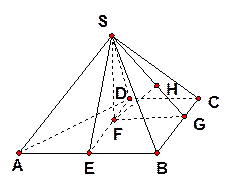
【分析】第(I)问的证明的突破口是利用等边三角形SAB这个条件,找出AB的中点E,连结SE,DE,就做出了解决这个问题的关键辅助线。
(II)本题直接找线面角不易找出,要找到与AB平行的其它线进行转移求解。
【命题意图】以四棱锥为载体考查线面垂直证明和线面角的计算,注重与平面几何的综合.
解法一:(Ⅰ)取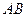 中点
中点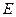 ,连结
,连结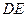 ,则四边形
,则四边形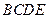 为矩形,
为矩形,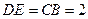 ,连结
,连结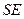 ,则
,则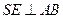 ,
,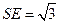 .
.
又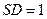 ,故
,故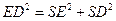 ,
,
所以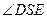 为直角. ………………3分
为直角. ………………3分
由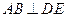 ,
,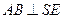 ,
,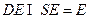 ,得
,得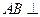 平面
平面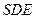 ,所以
,所以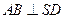 .
.
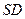 与两条相交直线
与两条相交直线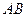 、
、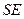 都垂直.
都垂直.
所以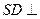 平面
平面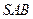 . ………………6分
. ………………6分
另解:由已知易求得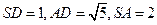 ,于是
,于是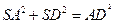 .可知
.可知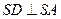 ,同理可得
,同理可得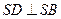 ,又
,又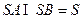 .所以
.所以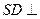 平面
平面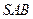 . ………………6分
. ………………6分
(Ⅱ)由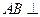 平面
平面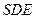 知,平面
知,平面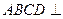 平面
平面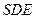 .
.
作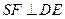 ,垂足为
,垂足为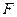 ,则
,则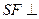 平面ABCD,
平面ABCD,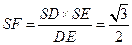 .
.
作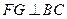 ,垂足为
,垂足为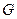 ,则
,则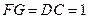 .
.
连结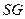 .则
.则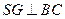 .
.
又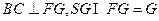 ,故
,故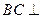 平面
平面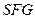 ,平面
,平面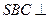 平面
平面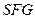 .……9分
.……9分
作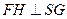 ,
,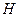 为垂足,则
为垂足,则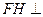 平面
平面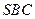 .
.
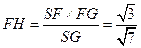 ,即
,即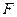 到平面
到平面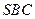 的距离为
的距离为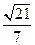 .
.
由于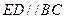 ,所以
,所以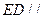 平面
平面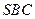 ,
,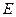 到平面
到平面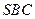 的距离
的距离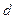 也为
也为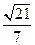 .
.
设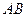 与平面
与平面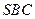 所成的角为
所成的角为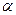 ,则
,则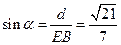 ,
,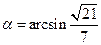 .……12分
.……12分
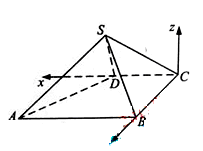
解法二:以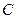 为原点,射线
为原点,射线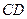 为
为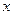 轴的正半轴,建立如图所示的空间直角坐标系
轴的正半轴,建立如图所示的空间直角坐标系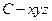 .
.
设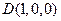 ,则
,则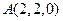 、
、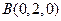 .
.
又设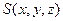 ,则
,则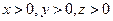 .
.
(Ⅰ)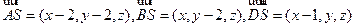 ,
,
由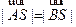 得
得
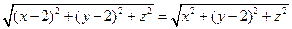 ,
,
故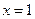 .
.
由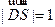 得
得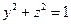 ,
,
又由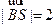 得
得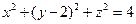 ,
,
即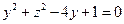 ,故
,故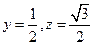 . ………………3分
. ………………3分
于是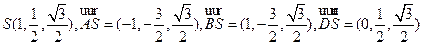 ,
,
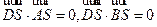 .
.
故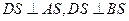 ,又
,又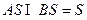 ,
,
所以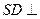 平面
平面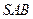 . ………………6分
. ………………6分
(Ⅱ)设平面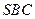 的法向量
的法向量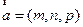 ,
,
则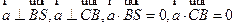 .
.
又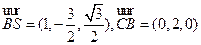 ,
,
故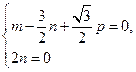 ………………9分
………………9分
取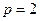 得
得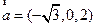 ,又
,又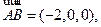
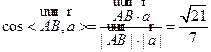 .
.
故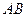 与平面
与平面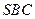 所成的角为
所成的角为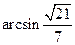 . ………………12分
. ………………12分












