(21)(本小题满分l2分)(注意:在试题卷上作答无效)
已知函数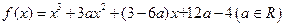

(Ⅰ)证明:曲线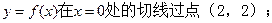
(Ⅱ)若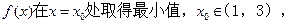 求a的取值范围.
求a的取值范围.
【分析】第(I)问直接利用导数的几何意义,求出切线的斜率,然后易写出切线方程.
(II)第(II)问是含参问题,关键是抓住方程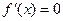 的判别式进行分类讨论.
的判别式进行分类讨论.
解:(I)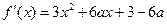 .………………2分
.………………2分
由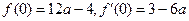 得曲线
得曲线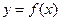 在x=0处的切线方程为
在x=0处的切线方程为
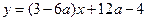
由此知曲线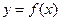 在x=0处的切线过点(2,2) .………………6分
在x=0处的切线过点(2,2) .………………6分
(II)由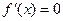 得
得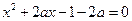 .
.
(i)当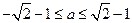 时,
时,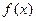 没有极小值; .………………8分
没有极小值; .………………8分
(ii)当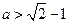 或
或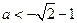 时,由
时,由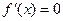 得
得
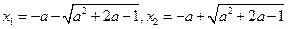
故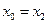 .由题设知
.由题设知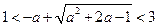 ,
,
当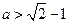 时,不等式
时,不等式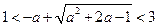 无解;
无解;
当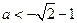 时,解不等式
时,解不等式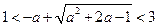 得
得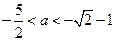
综合(i)(ii)得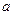 的取值范围是
的取值范围是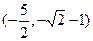 ..………………12分
..………………12分
(22)(本小题满分l2分)(注意:在试题卷上作答无效)
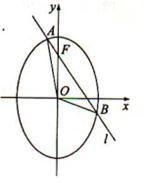
已知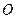 为坐标原点,
为坐标原点,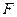 为椭圆
为椭圆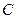 :
: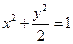 在
在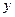 轴正半轴上的焦点,过
轴正半轴上的焦点,过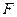 且斜率为
且斜率为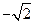 的直线
的直线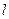 与
与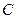 交与
交与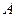 、
、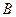 两点,点
两点,点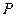 满
满 足
足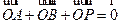 .
.
(I)证明:点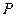 在
在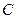 上;
上;
(II)设点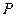 关于点
关于点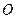 的对称点为
的对称点为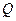 ,证明:
,证明: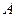 、
、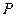 、
、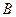 、
、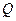 四点在同一圆上.
四点在同一圆上.
【命题意图】本题考查直线方程、平面向量的坐标运算、点与曲线的位置关系、曲线交点坐标求法及四点共圆的条件。
【分析】方程联立利用韦达定理是解决这类问题的基本思路,注意把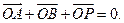 用坐标表示后求出P点的坐标,然后再结合直线方程把P点的纵坐标也用A、B两点的横坐标表示出来.从而求出点P的坐标代入椭圆方程验证即可证明点P在C上;(II)此问题证明有两种思路:思路一:关键是证明
用坐标表示后求出P点的坐标,然后再结合直线方程把P点的纵坐标也用A、B两点的横坐标表示出来.从而求出点P的坐标代入椭圆方程验证即可证明点P在C上;(II)此问题证明有两种思路:思路一:关键是证明 互补.通过证明这两个角的正切值互补即可,再求正切值时要注意利用到角公式.
互补.通过证明这两个角的正切值互补即可,再求正切值时要注意利用到角公式.
思路二:根据圆的几何性质圆心一定在弦的垂直平分线上,所以根据两条弦的垂直平分线的交点找出圆心N,然后证明N到四个点A、B、P、Q的距离相等即可.
【解析】(I)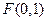 ,
,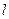 的方程为
的方程为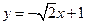 ,代入
,代入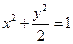 并化简得
并化简得
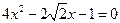 . …………………………2分
. …………………………2分
设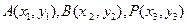 ,
,
则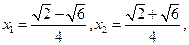
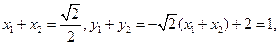
由题意得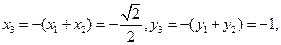
所以点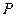 的坐标为
的坐标为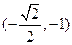 .
.
经验证点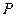 的坐标
的坐标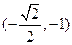 满足方程
满足方程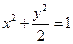 ,故点
,故点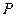 在椭圆
在椭圆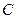 上 …6分
上 …6分
(II)由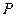
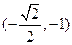 和题设知,
和题设知,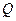
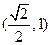 ,
,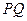 的垂直平分线
的垂直平分线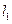 的方程为
的方程为
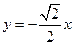 . ①
. ①
设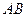 的中点为
的中点为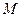 ,则
,则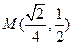 ,
,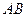 的垂直平分线
的垂直平分线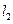 的方程为
的方程为
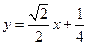 . ②
. ②
由①、②得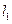 、
、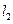 的交点为
的交点为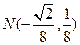 . …………………………9分
. …………………………9分
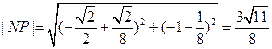 ,
,
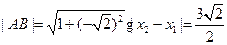 ,
,
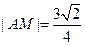 ,
,
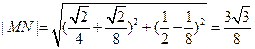 ,
,
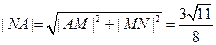 ,
,
故 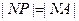 ,
,
又 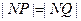 ,
, 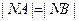 ,
,
所以 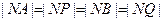 ,
,
由此知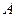 、
、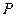 、
、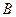 、
、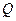 四点在以
四点在以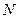 为圆心,
为圆心,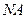 为半径的圆上. ……………12分
为半径的圆上. ……………12分
(II)法二: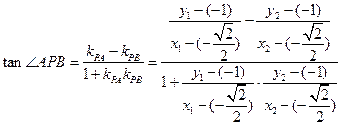
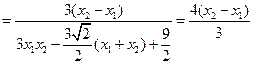
同理
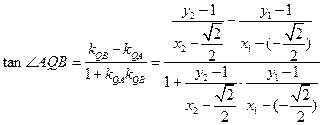
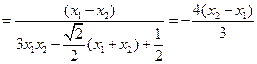
所以 互补,
互补,
因此A、P、B、Q四点在同一圆上。
【点评】本题涉及到平面向量,有一定的综合性和计算量,完成有难度. 首先出题位置和平时模拟几乎没有变化,都保持全卷倒数第二道题的位置,这点考生非常适应的。相对来讲比较容易,是因为这道题最好特点没有任何的未知参数,我们看这道题椭圆完全给出,直线过了椭圆焦点,并且斜率也给出,平时做题斜率不给出,需要通过一定条件求出来,或者根本求不出来,这道题都给了,反而同学不知道怎么下手,让我求什么不知道,给出马上给向量条件,出了两道证明题,这个跟平时做的不太一样,证明题结论给大家,需要大家严谨推导出来,可能叙述的时候有不严谨的地方。这两问出的非常巧妙,非常涉及解析几何本质的内容,一个证明点在椭圆上的问题,还有一个疑问既然出现四点共圆,这都是平时很少涉及内容。从侧面体现教育深层次的问题,让学生掌握解析几何的本质,而不是把套路解决。其实几年前上海考到解析几何本质问题,最后方法用代数方法研究几何的问题,什么是四点共圆?首先在同一个圆上,首先找到圆心,四个点找圆形不好找,最简单的两个点怎么找?这是平时的知识,怎么找距离相等的点,一定在中垂线,两个中垂线交点必然是圆心,找到圆心再距离四个点距离相等,这就是简单的计算问题.方法确定以后计算量其实比往年少.












