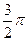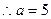
(17)(本小题满分12分)
本题考查椭圆的定义,椭圆的标准方程及其简单几何性质,直线的点斜式方程与一般方程,点到直线的距离公式等基础知识,考查解析几何的基本思想和综合运算能力。
解:(I)设椭圆E的方程为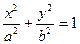
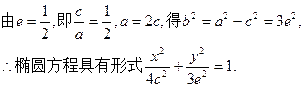
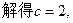
∴椭圆E的方程为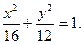
(II)由(I)知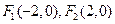 ,所以直线AF1的方程为:
,所以直线AF1的方程为:
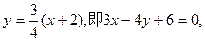
直线AF2的方程为: 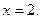
由椭圆E的图形知,∠F1AF2的 角平分线所在直线的斜率为正数,
角平分线所在直线的斜率为正数,
设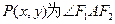 的角平分线所在直线上任一点,则
的角平分线所在直线上任一点,则
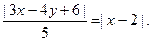
若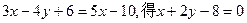 ,其斜率为负,不合题意,舍去.
,其斜率为负,不合题意,舍去.
于是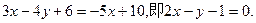
所以∠F1AF2的角平分线所在直线的方程为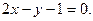
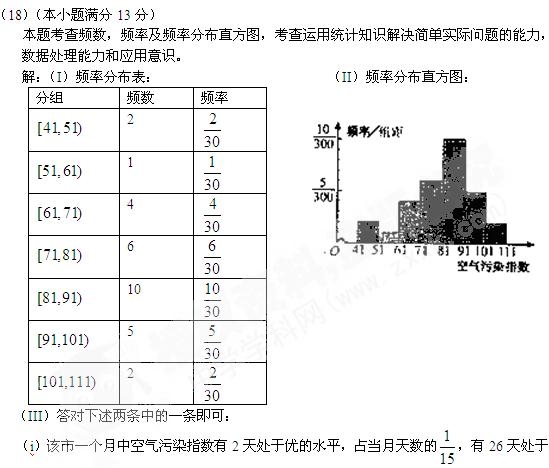 良的水平,占当月天数的
良的水平,占当月天数的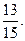 处于优或良的天数共有28天,占当月天数的
处于优或良的天数共有28天,占当月天数的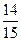 ,说明该市空气质量基本良好。
,说明该市空气质量基本良好。
(ii)轻微污染有2天,占当月天数的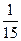 ,污染指数在80以上的接近轻微污染的天数有15天,加上处于轻微污染的天数,共有17天,占当月天数的
,污染指数在80以上的接近轻微污染的天数有15天,加上处于轻微污染的天数,共有17天,占当月天数的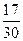 ,超过50%,说明该市空气质量有待进一步改善。
,超过50%,说明该市空气质量有待进一步改善。
(19)(本小题满分13分)
本题考查空间线面平行、线面垂直、面面垂直、体积的计算等基础知识,同时考查空间想象能力、推理论证能力和运算能力.
(1)证:设AC与BD交于点G,则G为AC的中点,连EG,GH,
由于H为BC的中点,
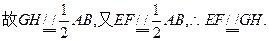
∴四边形EFHG为平行四边形,
∴EG//FH,而EG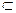 平面EDB,∴FH//平面EDB.
平面EDB,∴FH//平面EDB.
(II)证:由四边形ABCD为正方形,有AB⊥BC,
又EF//AB,
∴EF⊥BC.而EF⊥FB,∵EF⊥平面BFC,∴EF⊥FH,∴AB⊥FH.
又BF=FC,H为BC的中点,∴FH⊥BC.
∴FH⊥平面ABCD,
∴FH⊥AC,又FH//BC,∴AC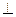 EG.
EG.
又AC⊥BD,EG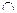 BD=G,∴AG⊥平面EDB.
BD=G,∴AG⊥平面EDB.
(III)解:∵EF⊥FB,∠BFC=90°,∴BF⊥平面CDEF,
∴BF为四面体B—DEF的高,又BC=AB=2,∴BF=FC=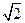
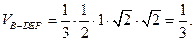
(20)(本小题满分12分)
本题考查导数的运算,利用导数研究函数的单调性与极值的方法,考查综合运用数学知识解决问题的能力。
解:由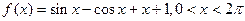 ,
,
知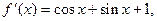
于是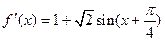
令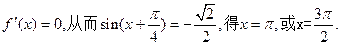
当x变化时,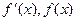 变化情况如下表:
变化情况如下表:
|
|
|
|
|
|
| + | 0 | — | 0 | + |
| 单调递增
|
|
|
| 单调递增
|
因此,由上表知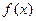 的单调递增区间是
的单调递增区间是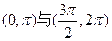 ,单调递减区间是
,单调递减区间是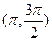 ,极小值为
,极小值为
(21)(本小题满分13分)
本题考查等比数列的基本知识,利用错位相减法求和等基本方法,考查抽象能力以及推理论证能力。
解:(I)将直线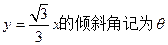 ,则有
,则有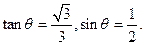
设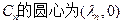 ,则由题意知
,则由题意知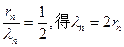 ;
;
同理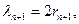
从而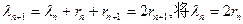 代入,
代入,
解得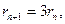
故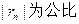
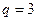 的等比数列。
的等比数列。
(II)由于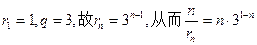 ,
,
| ① |
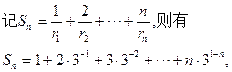
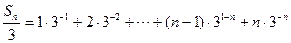 ②
②
①—②,得
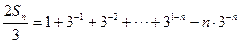
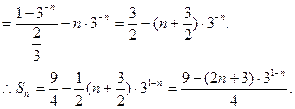



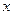
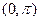
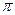
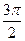
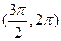
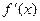
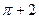
 单调递减
单调递减