(21)(本小题满分13)
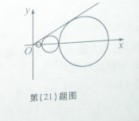
设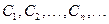 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在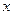 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线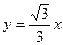 相切,对每一个正整数
相切,对每一个正整数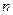 ,圆
,圆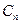 都与圆
都与圆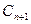 相互外切,以
相互外切,以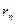 表示
表示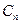 的半径,已知
的半径,已知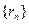 为递增数列。
为递增数列。
(Ⅰ)证明: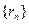 为等比数列;
为等比数列;
(Ⅱ)设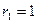 ,求数列
,求数列
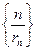 的前
的前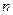 项和。
项和。
21.【命题意图】此题主要考查数列与几何图形的基础知识,运用错位相减法求数列和的能力
【解析】
解:(I)将直线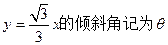 ,则有
,则有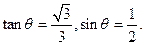
设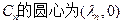 ,则由题意知
,则由题意知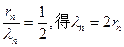 ;
;
同理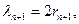
从而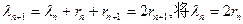 代入,
代入,
解得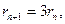
故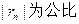
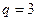 的等比数列。
的等比数列。
(II)由于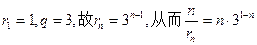 ,
,

【点评】数列的证明问题一般是从定义出发,如证明等比数列,则一般要满足“从第2项起,后一项与前一项之比为常数”;对于数列的求和则要根据数列的特征选择裂项法或错位相减法等.












