二、填空题(6小题,每小题3分)
13.(3分)(2013•眉山)函数y=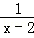 中,自变量x的取值范围是 x≠2 .
中,自变量x的取值范围是 x≠2 .
考点: 函数自变量的取值范围;分式有意义的条件.
专题: 计算题.
分析: 求函数自变量的取值范围,就是求函数解析式有意义的条件,分式有意义的条件是:分母不为0.
解答: 解:x﹣2≠0,解得x≠2.
点评: 本题考查的知识点为:分式有意义,分母不为0.
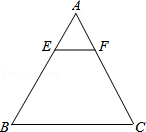
14.(3分)(2013•眉山)如图,△ABC中,E、F分别是AB、AC上的两点,且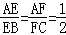 ,若△AEF的面积为2,则四边形EBCF的面积为 16 .
,若△AEF的面积为2,则四边形EBCF的面积为 16 .
考点: 相似三角形的判定与性质.
分析: 根据题意可判定△AEF∽△ABC,利用面积比等于相似比平方可得出△ABC的面积,继而根据S四边形EBCF=S△ABC﹣S△AEF,即可得出答案.
解答: 解:∵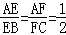 ,
,
∴EF∥BC,
∴△AEF∽△ABC,
∴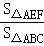 =(
=(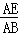 )2=(
)2=(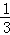 )2=
)2=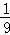 ,
,
∴S△ABC=18,
则S四边形EBCF=S△ABC﹣S△AEF=18﹣2=16.
故答案为:16.
点评: 本题考查了相似三角形的判定与性质,解答本题的关键是证明△AEF∽△ABC,要求同学们熟练掌握相似三角形的面积比等于相似比平方.
15.(3分)(2013•眉山)为筹备班级里的新年晚会,班长对全班同学爱吃哪几种水果作了民意调查,最终买什么水果,该由调查数据的 众数决定(在横线上填写:平均数或中位数或众数).
考点: 统计量的选择.
分析: 班长最值得关注的应该是哪种水果爱吃的人数最多,即众数.
解答: 解:平均数、中位数、众数是描述一组数据集中程度的统计量;既然是为筹备班级的初中毕业联欢会做准备,那么买的水果肯定是大多数人爱吃的才行,故最值得关注的是众数.
故答案为:众数.
点评: 此题主要考查统计的有关知识,主要包括平均数、中位数、众数的意义.反映数据集中程度的统计量有平均数、中位数、众数等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
16.(3分)(2013•眉山)已知关于x的一元二次方程x2﹣x﹣3=0的两个实数根分别为α、β,则(α+3)(β+3)= 9 .
考点: 根与系数的关系.
分析: 根据x的一元二次方程x2﹣x﹣3=0的两个实数根分别为α、β,求出α+β和αβ的值,再把要求的式子变形为αβ+3(α+β)+9,最后把α+β和αβ的值代入,计算即可.
解答: 解:∵x的一元二次方程x2﹣x﹣3=0的两个实数根分别为α、β,
∴α+β=1,αβ=﹣3,
∴(α+3)(β+3)=αβ+3α+3β+9=αβ+3(α+β)+9=﹣3+3×1+9=9;
故答案为:9.
点评: 此题考查了一元二次方程根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
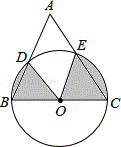
17.(3分)(2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为 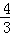 π .(结果保留π)
π .(结果保留π)
考点: 扇形面积的计算.
分析: 先根据三角形内角和定理得出∠ABC+∠ACB的度数,再由△OBD、△OCE是等腰三角形得出∠BDO+∠CEO的度数,由三角形内角和定理即可得出∠BOD+∠COD的度数,再根据扇形的面积公式即可得出结论.
解答: 解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵△OBD、△OCE是等腰三角形,
∴∠BDO+∠CEO=∠ABC+∠ACB=120°,
∴∠BOD+∠COE=360°﹣(∠BDO+∠CEO)﹣(∠ABC+∠ACB)=360°﹣120°﹣120°=120°,
∵BC=4,
∴OB=OC=2,
∴S阴影=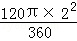 =
=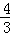 π.
π.
故答案为: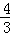 π.
π.
点评: 本题考查的是扇形面积的计算,解答此类问题时往往用到三角形的内角和是180°这一隐藏条件,要求同学们掌握扇形的面积公式.
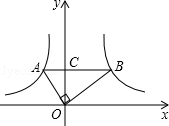
18.(3分)(2013•眉山)如图,在函数y1=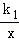 (x<0)和y2=
(x<0)和y2=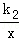 (x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=
(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=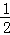 ,S△BOC=
,S△BOC=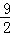 ,则线段AB的长度=
,则线段AB的长度= 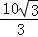 .
.
考点: 反比例函数系数k的几何意义.
专题: 计算题.
分析: 根据反比例函数y=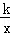 (k≠0)系数k的几何意义易得两反比例解析式为y=﹣
(k≠0)系数k的几何意义易得两反比例解析式为y=﹣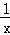 ,y=
,y=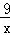 ,设B点坐标为(
,设B点坐标为(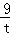 ,t)(t>0),则可表示出A点坐标为(﹣
,t)(t>0),则可表示出A点坐标为(﹣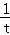 ,t),然后证明Rt△AOC∽Rt△OBC,得到OC:BC=AC:BC,即t:
,t),然后证明Rt△AOC∽Rt△OBC,得到OC:BC=AC:BC,即t: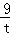 =
=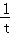 :t,解得t=
:t,解得t=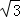 ,再确定A、B点的坐标,最后用两点的横坐标之差来得到线段AB的长.
,再确定A、B点的坐标,最后用两点的横坐标之差来得到线段AB的长.
解答: 解:∵S△AOC=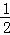 ,S△BOC=
,S△BOC=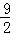 ,
,
∴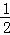 |k1|=
|k1|=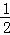 ,
,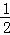 |k2|=
|k2|=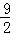 ,
,
∴k1=﹣1,k2=9,
∴两反比例解析式为y=﹣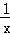 ,y=
,y=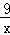 ,
,
设B点坐标为(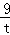 ,t)(t>0),
,t)(t>0),
∵AB∥x轴,
∴A点的纵坐标为t,
把y=t代入y=﹣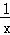 得x=﹣
得x=﹣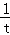 ,
,
∴A点坐标为(﹣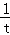 ,t),
,t),
∵OA⊥OB,
∴∠AOC=∠OBC,
∴Rt△AOC∽Rt△OBC,
∴OC:BC=AC:BC,即t: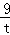 =
=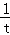 :t,
:t,
∴t=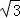 ,
,
∴A点坐标为(﹣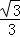 ,
,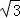 ),B点坐标为(3
),B点坐标为(3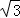 ,
,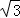 ),
),
∴线段AB的长度=3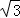 ﹣(﹣
﹣(﹣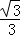 )=
)=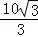 .
.
故答案为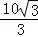 .
.
点评: 本题考查了反比例函数y=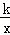 (k≠0)系数k的几何意义:从反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=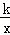 (k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.












