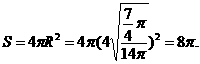一.选择题
(1)已知全集U={1,2,3,4,5,6,7,8},M ={1,3,5,7},N ={5,6,7},则Cu( M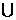 N)=
N)=
(A) {5,7} (B) {2,4} (C){2.4.8} (D){1,3,5,6,7}
答案:C
解析:本题考查集合运算能力。
(2)函数y=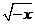 (x
(x 0)的反函数是
0)的反函数是
(A)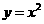 (x
(x 0) (B)
0) (B)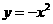 (x
(x 0)
0)
(B)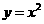 (x
(x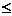 0) (D)
0) (D)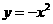 (x
(x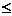 0)
0)
答案:B
解析:本题考查反函数概念及求法,由原函数x 0可知AC错,原函数y
0可知AC错,原函数y 0可知D错,选B.
0可知D错,选B.
(3) 函数y=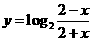 的图像
的图像
(A) 关于原点对称 (B)关于主线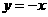 对称
对称
(C) 关于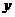 轴对称 (D)关于直线
轴对称 (D)关于直线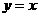 对称
对称
答案:A
解析:本题考查对数函数及对称知识,由于定义域为(-2,2)关于原点对称,又f(-x)=-f(x),故函数为奇函数,图像关于原点对称,选A。
(4)已知△ABC中,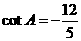 ,则
,则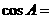
(A)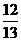 (B)
(B)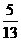 (C)
(C)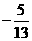 (D)
(D)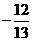
答案:D
解析:本题考查同角三角函数关系应用能力,先由cotA=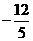 知A为钝角,cosA<0排除a和b,再由
知A为钝角,cosA<0排除a和b,再由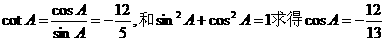 选D
选D
(5) 已知正四棱柱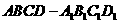 中,
中,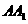 =
=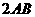 ,
,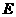 为
为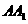 重点,则异面直线
重点,则异面直线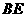
与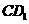 所形成角的余弦值为
所形成角的余弦值为
(A)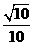 (B)
(B)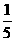 (C)
(C)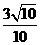 (D)
(D)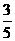
答案:C
解析:本题考查异面直线夹角求法,方法一:利用平移,CD’∥BA' ,因此求△EBA'中∠A'BE即可,易知EB=
,因此求△EBA'中∠A'BE即可,易知EB=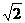 ,A'E=1,A'B=
,A'E=1,A'B=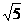 ,故由余弦定理求cos∠A'BE=
,故由余弦定理求cos∠A'BE=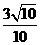 ,或由向量法可求。
,或由向量法可求。
(6) 已知向量a = (2,1), a·b = 10,︱a + b ︱=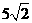 ,则︱b ︱=
,则︱b ︱=
(A)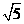 (B)
(B)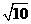 (C)5 (D)25
(C)5 (D)25
答案:C
解析:本题考查平面向量数量积运算和性质,由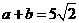 知(a+b)2=a2+b2+2ab=50,得|b|=5 选C。
知(a+b)2=a2+b2+2ab=50,得|b|=5 选C。
(7)设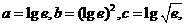 则
则
(A)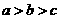 (B)
(B)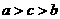 (C)
(C)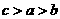 (D)
(D)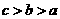
答案:B
解析:本题考查对数函数的增减性,由1>lge>0,知a>b,又c=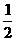 lge, 作商比较知c>b,选B。
lge, 作商比较知c>b,选B。
(8)双曲线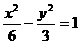 的渐近线与圆
的渐近线与圆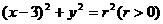 相切,则r=
相切,则r=
(A)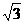 (B)2 (C)3 (D)6
(B)2 (C)3 (D)6
答案:A
解析:本题考查双曲线性质及圆的切线知识,由圆心到渐近线的距离等于r,可求r=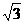
(9)若将函数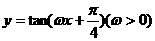 的图像向右平移
的图像向右平移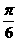 个单位长度后,与函数
个单位长度后,与函数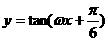 的图像重合,则
的图像重合,则 的最小值为
的最小值为
(A)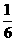 (B)
(B)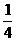 (C)
(C)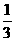 (D)
(D)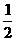

答案:D
解析:本题考查正切函数图像及图像平移,由平移及周期性得出ωmin=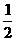
(10)甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有
(A)6种 (B)12种 (C)24种 (D)30种
答案:C
解析:本题考查分类与分步原理及组合公式的运用,可先求出所有两人各选修2门的种数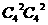 =36,再求出两人所选两门都相同和都不同的种数均为
=36,再求出两人所选两门都相同和都不同的种数均为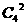 =6,故只恰好有1门相同的选法有24种 。
=6,故只恰好有1门相同的选法有24种 。
(11)已知直线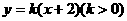 与抛物线C:
与抛物线C: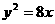 相交A、B两点,F为C的焦点。若
相交A、B两点,F为C的焦点。若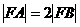 ,则k=
,则k=
(A)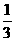 (B)
(B)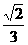 (C)
(C)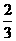 (D)
(D)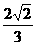
答案:D
解析:本题考查抛物线的第二定义,由直线方程知直线过定点即抛物线焦点(2,0),由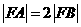 及第二定义知
及第二定义知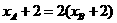 联立方程用根与系数关系可求k=
联立方程用根与系数关系可求k=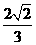 。
。
(12)纸质的正方体的六个面根据其方位分别标记为上、下、东、南、西、北。现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到右侧的平面图形,则标“△”的面的方位是
(A)南 (B)北 (C)西 (D)下
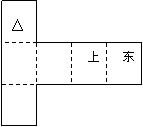
答案:B
解析:.此题用还原立体图方法直接得出结果,使上在正上方依次找到对应面即可。
第Ⅱ卷(非选择题)
本卷共10小题,共90分。
二.填空题:本大题共4小题,每小题5分,共20分。把答案填写在答题卡上相应位置的横线上.
(13)设等比数列{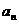 }的前n项和为
}的前n项和为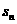 。若
。若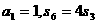 ,则
,则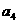 = ×
= ×
答案:3
解析:本题考查等比数列的性质及求和运算,由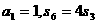 得q3=3故a4=a1q3=3。
得q3=3故a4=a1q3=3。
(14)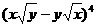 的展开式中
的展开式中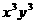 的系数为 ×
的系数为 × 

答案:6
解析:本题考查二项展开式,直接用公式展开,注意根式的化简。
(15)已知圆O: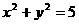 和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于 ×
和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于 ×
答案: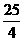
解析:由题意可直接求出切线方程为y-2=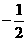 (x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和
(x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和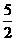 ,所以所求面积为
,所以所求面积为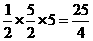 。
。
(16)设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C。若圆C的面积等于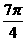 ,则球O的表面积等于 ×
,则球O的表面积等于 ×
答案:8π
解析:本题考查立体几何球面知识,注意结合平面几何知识进行运算,由