(20)(本小题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核。
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;
(Ⅲ)求抽取的4名工人中恰有2名男工人的概率。
解析:本题考查概率统计知识,要求有正确理解分层抽样的方法及利用分类原理处理事件概率的能力,第一问直接利用分层统计原理即可得人数,第二问注意要用组合公式得出概率,第三问关键是理解清楚题意以及恰有2名男工人的具体含义,从而正确分类求概率。
解:(I)由于甲、乙两组各有10名工人,根据分层抽样原理,要从甲、乙两组中共抽取4名工人进行技术考核,则从每组各抽取2名工人。
(II)记 表示事件:从甲组抽取的工人中恰有1名女工人,则
表示事件:从甲组抽取的工人中恰有1名女工人,则
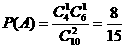

(III)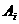 表示事件:从甲组抽取的2名工人中恰有
表示事件:从甲组抽取的2名工人中恰有 名男工人,
名男工人,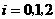
 表示事件:从乙组抽取的2名工人中恰有
表示事件:从乙组抽取的2名工人中恰有 名男工人,
名男工人,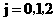
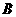 表示事件:抽取的4名工人中恰有2名男工人。
表示事件:抽取的4名工人中恰有2名男工人。
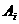 与
与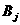 独立,
独立,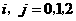 ,且
,且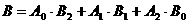
故 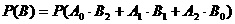
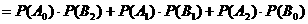
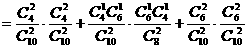
(21)(本小题满分12分)
| 设函数 ,其中常数a>1 |
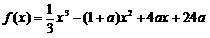
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若当x≥0时,f(x)>0恒成立,求a的取值范围。
解析:本题考查导数与函数的综合运用能力,涉及利用导数讨论函数的单调性,第一问关键是通过分析导函数,从而确定函数的单调性,第二问是利用导数及函数的最值,由恒成立条件得出不等式条件从而求出的范围。
解: (I)

由 知,当
知,当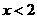 时,
时, ,故
,故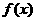 在区间
在区间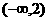 是增函数;
是增函数;
当 时,
时,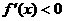 ,故
,故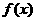 在区间
在区间 是减函数;
是减函数;
当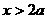 时,
时, ,故
,故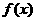 在区间
在区间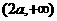 是增函数。
是增函数。
综上,当 时,
时,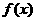 在区间
在区间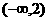 和
和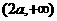 是增函数,在区间
是增函数,在区间 是减函数。
是减函数。
(II)由(I)知,当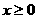 时,
时,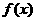 在
在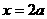 或
或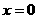 处取得最小值。
处取得最小值。
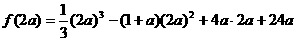
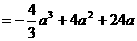

由假设知 即
即 解得 1
解得 1
故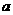 的取值范围是(1,6)
的取值范围是(1,6)
(22)(本小题满分12分)
已知椭圆C: 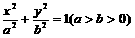 的离心率为 的离心率为 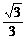 ,过右焦点F的直线l与C相交于A、B ,过右焦点F的直线l与C相交于A、B |
| 两点,当l的斜率为1时,坐标原点O到l的距离为
|
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有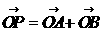 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
解析:本题考查解析几何与平面向量知识综合运用能力,第一问直接运用点到直线的距离公式以及椭圆有关关系式计算,第二问利用向量坐标关系及方程的思想,借助根与系数关系解决问题,注意特殊情况的处理。
解:(Ⅰ)设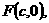 当
当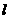 的斜率为1时,其方程为
的斜率为1时,其方程为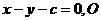 到
到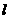 的距离为
的距离为

故  ,
,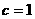
由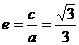
得 ,
,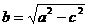 =
=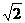
(Ⅱ)C上存在点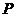 ,使得当
,使得当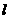 绕
绕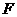 转到某一位置时,有
转到某一位置时,有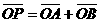 成立。
成立。
由 (Ⅰ)知C的方程为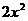 +
+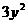 =6. 设
=6. 设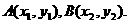
(ⅰ)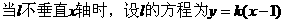
C 成立的充要条件是
成立的充要条件是 , 且
, 且
整理得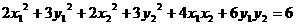
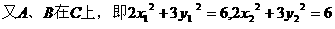
故  ①
①
将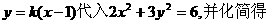
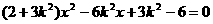
于是 ,
,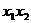 =
=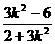 ,
,
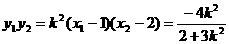
代入①解得, ,此时
,此时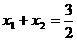
于是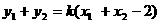 =
=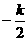 , 即
, 即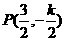
因此, 当 时,
时, ,
,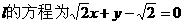 ;
;
当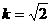 时,
时,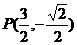 ,
,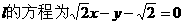 。
。
(ⅱ)当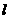 垂直于
垂直于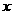 轴时,由
轴时,由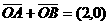 知,C上不存在点P使
知,C上不存在点P使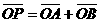 成立。
成立。
综上,C上存在点 使
使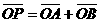 成立,此时
成立,此时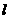 的方程为
的方程为