一、选择题:
1.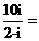
A.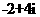 B.
B.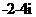 C.
C.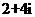 D.
D.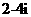
解:原式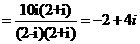 .故选A.
.故选A.
2. 设集合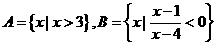 ,则
,则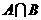 =
=
A.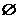 B.
B.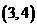 C.
C.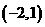 D.
D.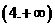
解: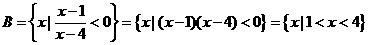 .
.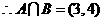 .故选B.
.故选B.
3. 已知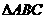 中,
中,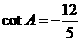 , 则
, 则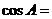
A.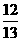 B.
B.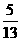 C.
C.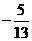 D.
D.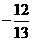
解:已知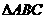 中,
中,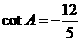 ,
,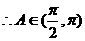 .
.
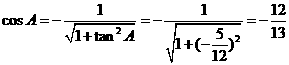 故选D.
故选D.
4.曲线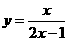 在点
在点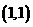 处的切线方程为
处的切线方程为 
A.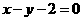 B.
B.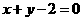 C.
C.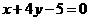 D.
D.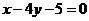
解: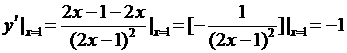 ,
,
故切线方程为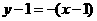 ,即
,即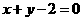 故选B.
故选B.
5. 已知正四棱柱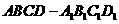 中,
中,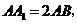
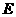 为
为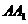 中点,则异面直线
中点,则异面直线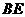 与
与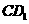 所成的角的余弦值为
所成的角的余弦值为
A.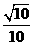 B.
B.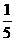 C.
C.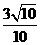 D.
D.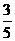
解:令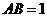 则
则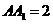 ,连
,连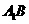
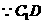 ∥
∥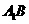
 异面直线
异面直线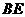 与
与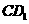 所成的角即
所成的角即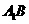
与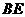 所成的角。在
所成的角。在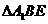 中由余弦定理易得
中由余弦定理易得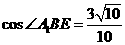 。故选C
。故选C
6. 已知向量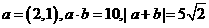 ,则
,则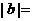

A.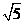 B.
B.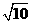 C.
C.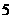 D.
D.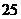
解: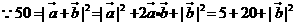
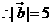 。故选C
。故选C
7. 设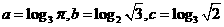 ,则
,则
A.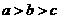 B.
B.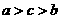 C.
C.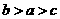 D.
D.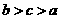
解: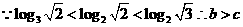
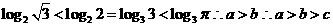 .故选A.
.故选A.
8. 若将函数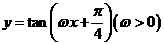 的图像向右平移
的图像向右平移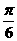 个单位长度后,与函数
个单位长度后,与函数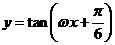 的图像重合,则
的图像重合,则 的最小值为
的最小值为
A.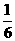 B.
B.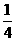 C.
C.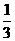 D.
D.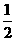
解: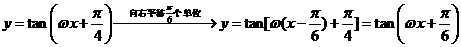
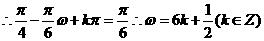 ,
,
又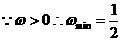 .故选D
.故选D
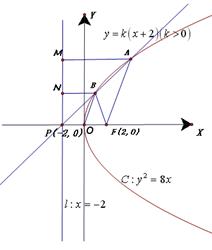
9. 已知直线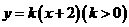 与抛物线
与抛物线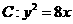 相交于
相交于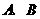 两点,
两点,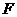 为
为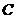 的焦点,若
的焦点,若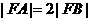 ,则
,则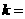
A.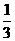 B.
B.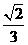 C.
C.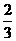 D.
D.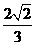
解:设抛物线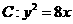 的准线为
的准线为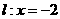 直线
直线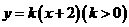 恒过定点P
恒过定点P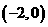 .如图过
.如图过 分 别作
分 别作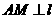 于
于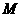 ,
,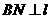 于
于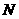 , 由
, 由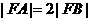 ,则
,则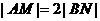 ,点B为AP的中点.连结
,点B为AP的中点.连结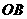 ,则
,则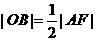 ,
,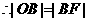 点
点 的横坐标为
的横坐标为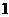 , 故点
, 故点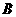 的坐标为
的坐标为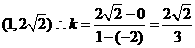 , 故选D
, 故选D
10. 甲、乙两人从4门课程中各选修2门。则甲、乙所选的课程中至少有1门不相同的选法共有
A. 6种 B. 12种 C. 30种 D. 36种
解:用间接法即可.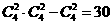 种. 故选C
种. 故选C
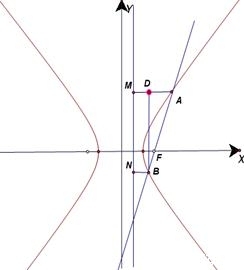
11. 已知双曲线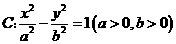 的右焦点为
的右焦点为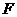 ,过
,过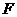 且斜率为
且斜率为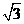 的直线交
的直线交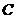 于
于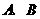 两点,若
两点,若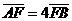 ,则
,则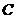 的离心率为
的离心率为
A.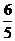 B.
B.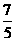 C.
C.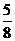 D.
D.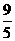
解:设双曲线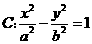 的右准线为
的右准线为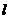 ,过
,过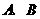 分 别作
分 别作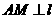 于
于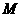 ,
,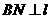 于
于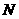 ,
,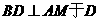 ,由直线AB的斜率为
,由直线AB的斜率为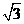 ,知直线AB的倾斜角为
,知直线AB的倾斜角为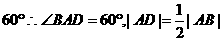 ,
,
由双曲线的第二定义有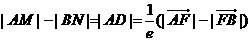
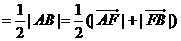 .
.
又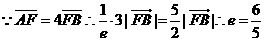 故选A
故选A
12.纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北。现有沿该正方体的一些棱将正方体剪开、外面朝上展平,得到右侧的平面图形,则标“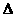 ”的面的方位是
”的面的方位是
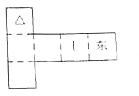
A. 南 B. 北
C. 西 D. 下
解:展、折问题。易判断选B