第II卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分。把答案填在答题卡上。
13.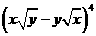 的展开式中
的展开式中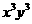 的系数为 6 。
的系数为 6 。
解: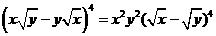 ,只需求
,只需求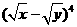 展开式中的含
展开式中的含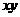 项的系数:
项的系数: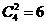

14. 设等差数列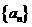 的前
的前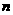 项和为
项和为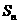 ,若
,若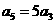 则
则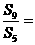 9 .
9 .
解: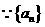 为等差数列,
为等差数列,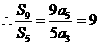
15.设 是球
是球 的半径,
的半径, 是
是 的中点,过
的中点,过 且与
且与 成45°角的平面截球
成45°角的平面截球 的表面得到圆
的表面得到圆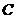 。若圆
。若圆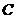 的面积等于
的面积等于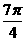 ,则球
,则球 的表面积等于
的表面积等于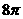 .
.
解:设球半径为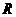 ,圆
,圆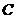 的半径为
的半径为 ,
,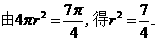
因为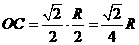 。由
。由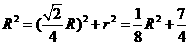 得
得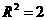 .故球
.故球 的表面积等于
的表面积等于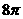 .
.
16. 已知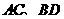 为圆
为圆 :
: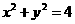 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为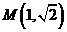 ,则四边形
,则四边形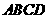 的面积的最大值为 。
的面积的最大值为 。
解:设圆心 到
到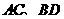 的距离分别为
的距离分别为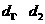 ,则
,则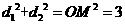 .
.
四边形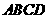 的面积
的面积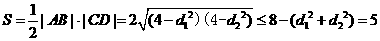
三、解答题:本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤
17(本小题满分10分)
设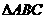 的内角
的内角 、
、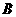 、
、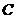 的对边长分别为
的对边长分别为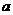 、
、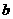 、
、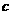 ,
,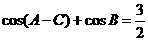 ,
,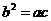 ,求
,求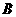 。
。
分析:由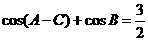 ,易想到先将
,易想到先将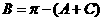 代入
代入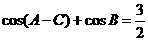 得
得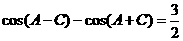 。然后利用两角和与差的余弦公式展开得
。然后利用两角和与差的余弦公式展开得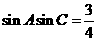 ;又由
;又由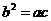 ,利用正弦定理进行边角互化,得
,利用正弦定理进行边角互化,得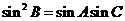 ,进而得
,进而得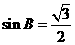 .故
.故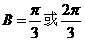 。大部分考生做到这里忽略了检验,事实上,当
。大部分考生做到这里忽略了检验,事实上,当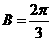 时,由
时,由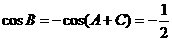 ,进而得
,进而得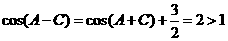 ,矛盾,应舍去。
,矛盾,应舍去。
也可利用若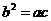 则
则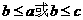 从而舍去
从而舍去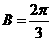 。不过这种方法学生不易想到。
。不过这种方法学生不易想到。
评析:本小题考生得分易,但得满分难。
18(本小题满分12分)
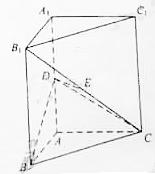
如图,直三棱柱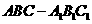 中,
中,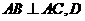 、
、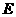 分别为
分别为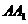 、
、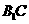 的中点,
的中点,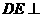 平面
平面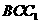
(I)证明: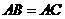
(II)设二面角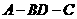 为60°,求
为60°,求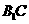 与平面
与平面 所成的角的大小。
所成的角的大小。
(I)分析一:连结BE,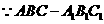 为直三棱柱,
为直三棱柱,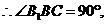
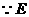 为
为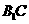 的中点,
的中点,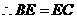 。又
。又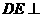 平面
平面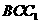 ,
,
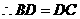 (射影相等的两条斜线段相等)而
(射影相等的两条斜线段相等)而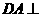 平面
平面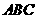 ,
,
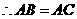 (相等的斜线段的射影相等)。
(相等的斜线段的射影相等)。
分析二:取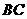 的中点
的中点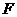 ,证四边形
,证四边形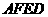 为平行四边形,进而证
为平行四边形,进而证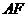 ∥
∥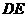 ,
,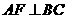 ,得
,得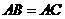 也可。
也可。
分析三:利用空间向量的方法。具体解法略。
(II)分析一:求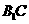 与平面
与平面 所成的线面角,只需求点
所成的线面角,只需求点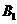 到面
到面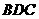 的距离即可。
的距离即可。

作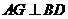 于
于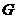 ,连
,连 ,则
,则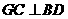 ,
, 为二面角
为二面角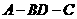 的平面角,
的平面角,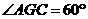 .不妨设
.不妨设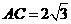 ,则
,则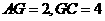 .在
.在 中,由
中,由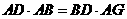 ,易得
,易得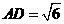 .
.
设点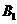 到面
到面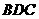 的距离为
的距离为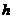 ,
,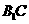 与平面
与平面 所成的角为
所成的角为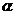 。利用
。利用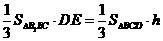 ,可求得
,可求得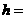
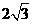 ,又可求得
,又可求得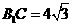
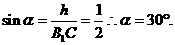
即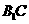 与平面
与平面 所成的角为
所成的角为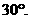
分析二:作出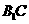 与平面
与平面 所成的角再行求解。如图可证得
所成的角再行求解。如图可证得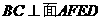 ,所以面
,所以面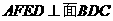 。由分析一易知:四边形
。由分析一易知:四边形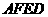 为正方形,连
为正方形,连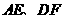 ,并设交点为
,并设交点为 ,则
,则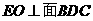 ,
, 为
为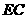 在面
在面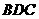 内的射影。
内的射影。 。以下略。
。以下略。
分析三:利用空间向量的方法求出面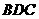 的法向量
的法向量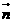 ,则
,则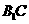 与平面
与平面 所成的角即为
所成的角即为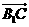 与法向量
与法向量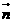 的夹角的余角。具体解法详见高考试题参考答案。
的夹角的余角。具体解法详见高考试题参考答案。
总之在目前,立体几何中的两种主要的处理方法:传统方法与向量的方法仍处于各自半壁江山的状况。命题人在这里一定会兼顾双方的利益。
19(本小题满分12分)
设数列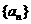 的前
的前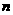 项和为
项和为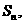 已知
已知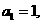
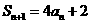
(I)设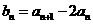 ,证明数列
,证明数列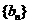 是等比数列
是等比数列
(II)求数列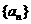 的通项公式。
的通项公式。
解:(I)由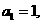 及
及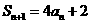 ,有
,有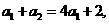
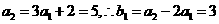
由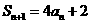 ,...① 则当
,...① 则当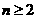 时,有
时,有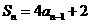 .....②
.....②
②-①得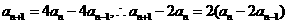
又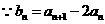 ,
,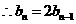
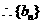 是首项
是首项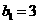 ,公比为2的等比数列.
,公比为2的等比数列.
(II)由(I)可得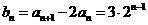 ,
,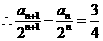
 数列
数列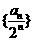 是首项为
是首项为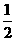 ,公差为
,公差为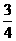 的等比数列.
的等比数列.

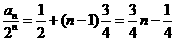 ,
,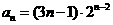
评析:第(I)问思路明确,只需利用已知条件寻找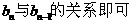 .
.
第(II)问中由(I)易得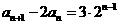 ,这个递推式明显是一个构造新数列的模型:
,这个递推式明显是一个构造新数列的模型: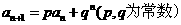 ,主要的处理手段是两边除以
,主要的处理手段是两边除以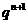 .
.