20.(本小题满分12分)
等比数列{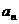 }的前n项和为
}的前n项和为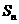 , 已知对任意的
, 已知对任意的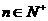 ,点
,点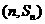 ,均在函数
,均在函数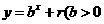 且
且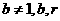 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(11)当b=2时,记 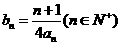 求数列
求数列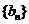 的前
的前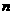 项和
项和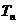
解:因为对任意的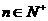 ,点
,点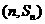 ,均在函数
,均在函数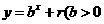 且
且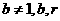 均为常数)的图像上.所以得
均为常数)的图像上.所以得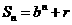 ,
,
当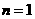 时,
时,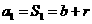 ,
,
当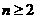 时,
时,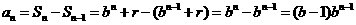 ,
,
又因为{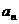 }为等比数列, 所以
}为等比数列, 所以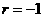 , 公比为
, 公比为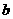 , 所以
, 所以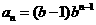
(2)当b=2时,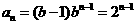 ,
, 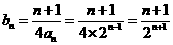
则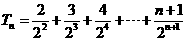
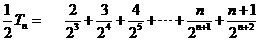
相减,得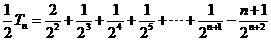
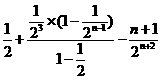
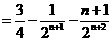
所以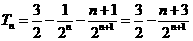
21.(本小题满分12分)
已知函数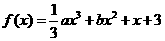 ,其中
,其中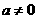
(1) 当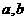 满足什么条件时,
满足什么条件时,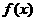 取得极值?
取得极值?
(2) 已知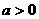 ,且
,且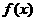 在区间
在区间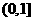 上单调递增,试用
上单调递增,试用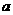 表示出
表示出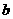 的取值范围.
的取值范围.
解: (1)由已知得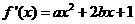 ,令
,令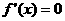 ,得
,得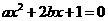 ,
,
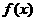 要取得极值,方程
要取得极值,方程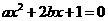 必须有解,
必须有解,
所以△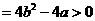 ,即
,即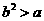 , 此时方程
, 此时方程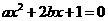 的根为
的根为
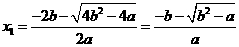 ,
,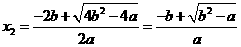 ,
,
所以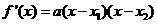
当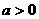 时,
时,
x | (-∞,x1) | x 1 | (x1,x2) | x2 | (x2,+∞) |
f’(x) | + | 0 | - | 0 | + |
f (x) | 增函数 | 极大值 | 减函数 | 极小值 | 增函数 |
所以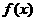 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
当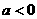 时,
时,
x | (-∞,x2) | x 2 | (x2,x1) | x1 | (x1,+∞) |
f’(x) | - | 0 | + | 0 | - |
f (x) | 减函数 | 极小值 | 增函数 | 极大值 | 减函数 |
所以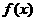 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
综上,当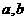 满足
满足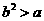 时,
时, 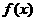 取得极值.
取得极值.
(2)要使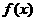 在区间
在区间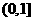 上单调递增,需使
上单调递增,需使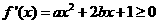 在
在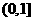 上恒成立.
上恒成立.
即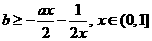 恒成立, 所以
恒成立, 所以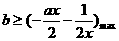
设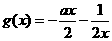 ,
,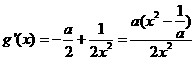 ,
,
令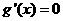 得
得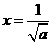 或
或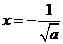 (舍去),
(舍去),
当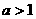 时,
时,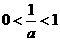 ,当
,当 时
时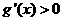 ,
,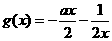 单调增函数;
单调增函数;
当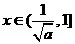 时
时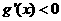 ,
,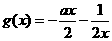 单调减函数,
单调减函数,
所以当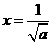 时,
时,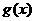 取得最大,最大值为
取得最大,最大值为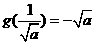 .
.
所以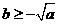
当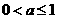 时,
时,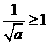 ,此时
,此时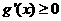 在区间
在区间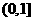 恒成立,所以
恒成立,所以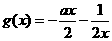 在区间
在区间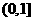 上单调递增,当
上单调递增,当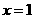 时
时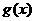 最大,最大值为
最大,最大值为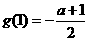 ,所以
,所以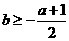
综上,当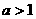 时,
时, 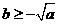 ; 当
; 当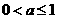 时,
时, 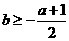
22. (本小题满分14分)
设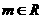 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量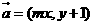 ,向量
,向量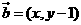 ,
,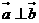 ,动点
,动点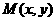 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知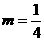 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且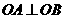 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知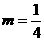 ,设直线
,设直线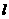 与圆C:
与圆C: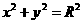 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且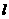 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
解:(1)因为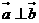 ,
,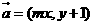 ,
,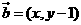 ,
,
所以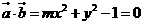 , 即
, 即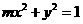 .
.
当m=0时,方程表示两直线,方程为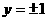 ;
;
当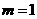 时, 方程表示的是圆
时, 方程表示的是圆
当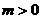 且
且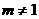 时,方程表示的是椭圆;
时,方程表示的是椭圆;
当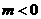 时,方程表示的是双曲线.
时,方程表示的是双曲线.
(2).当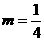 时, 轨迹E的方程为
时, 轨迹E的方程为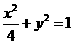 ,设圆心在原点的圆的一条切线为
,设圆心在原点的圆的一条切线为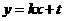 ,解方程组
,解方程组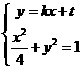 得
得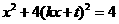 ,即
,即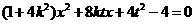 ,
,
要使切线与轨迹E恒有两个交点A,B,
则使△=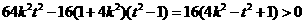 ,
,
即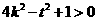 ,即
,即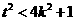 , 且
, 且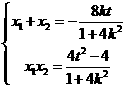
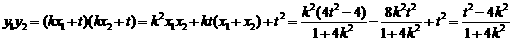 ,
,
要使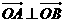 , 需使
, 需使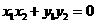 ,即
,即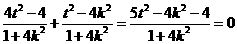 ,
,
所以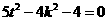 , 即
, 即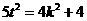 且
且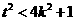 , 即
, 即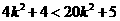 恒成立.
恒成立.
所以又因为直线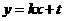 为圆心在原点的圆的一条切线,
为圆心在原点的圆的一条切线,
所以圆的半径为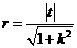 ,
,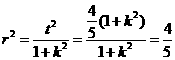 , 所求的圆为
, 所求的圆为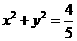 .
.
当切线的斜率不存在时,切线为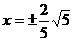 ,与
,与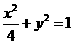 交于点
交于点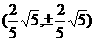 或
或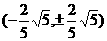 也满足
也满足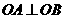 .
.
综上, 存在圆心在原点的圆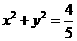 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且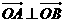 .
.
(3)当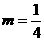 时,轨迹E的方程为
时,轨迹E的方程为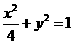 ,设直线
,设直线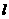 的方程为
的方程为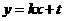 ,因为直线
,因为直线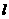 与圆C:
与圆C: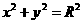 (1<R<2)相切于A1, 由(2)知
(1<R<2)相切于A1, 由(2)知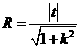 , 即
, 即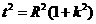 ①,
①,
因为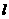 与轨迹E只有一个公共点B1,
与轨迹E只有一个公共点B1,
由(2)知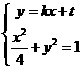 得
得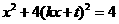 ,
,
即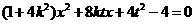 有唯一解
有唯一解
则△=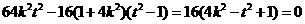 , 即
, 即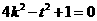 , ②
, ②
由①②得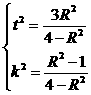 , 此时A,B重合为B1(x1,y1)点,
, 此时A,B重合为B1(x1,y1)点,
由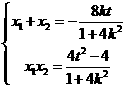 中
中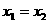 ,所以,
,所以,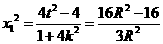 ,
,
B1(x1,y1)点在椭圆上,所以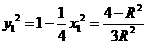 ,所以
,所以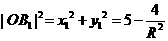 ,
,
在直角三角形OA1B1中,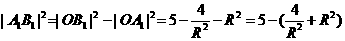 因为
因为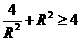 当且仅当
当且仅当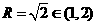 时取等号,所以
时取等号,所以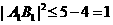 ,即
,即
当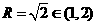 时|A1B1|取得最大值,最大值为1.
时|A1B1|取得最大值,最大值为1.












