文科数学参考答案
一、选择题:本大题共12小题,每小题5分,共60分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | A | D | B | A | C | C | B | C | C | D | B | A |
1. 由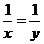 得
得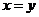 ,而由
,而由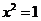 得
得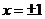 ,由
,由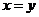 ,
,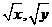 不一定有意义,而
不一定有意义,而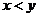 得不到
得不到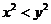
故选A.
2. 由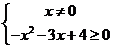 得
得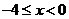 或
或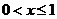 ,故选D.
,故选D.
3. 仅参加了一项活动的学生人数=50-(30+25-50)=45, 故选B.
4. 由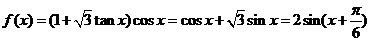 可得最小正周期为
可得最小正周期为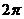 ,故选A.
,故选A.
5.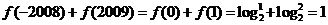 ,故选C.
,故选C.
6.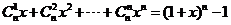 ,当
,当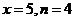 时,
时,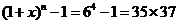 能被7整除, 故选C.
能被7整除, 故选C.
7. 由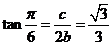 有
有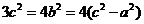 ,则
,则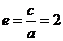 ,故选B.
,故选B.
8. 由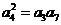 得
得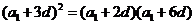 得
得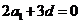 ,再由
,再由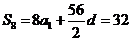 得
得 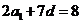 则
则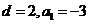 ,所以
,所以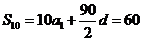 ,.故选C
,.故选C
9. 由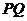 ∥
∥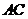 ,
,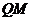 ∥
∥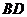 ,
,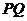 ⊥
⊥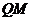 可得
可得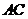 ⊥
⊥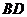 ,故
,故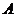 正确;
正确;
由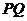 ∥
∥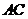 可得
可得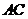 ∥截面
∥截面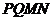 ,故
,故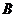 正确
正确
异面直线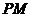 与
与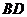 所成的角等于
所成的角等于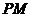 与
与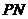 所成的角,故
所成的角,故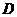 正确;
正确;
综上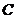 是错误的,故选
是错误的,故选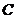 .
.
10. 所有可能的比赛分组情况共有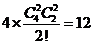 种,甲乙相遇的分组情况恰好有6种,故选
种,甲乙相遇的分组情况恰好有6种,故选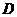 .
.
11. 由图可知,当质点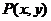 在两个封闭曲线上运动时,投影点
在两个封闭曲线上运动时,投影点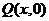 的速度先由正到0、到负数,再到0,到正,故
的速度先由正到0、到负数,再到0,到正,故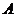 错误;质点
错误;质点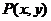 在终点的速度是由大到小接近0,故
在终点的速度是由大到小接近0,故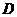 错误;质点
错误;质点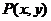 在开始时沿直线运动,故投影点
在开始时沿直线运动,故投影点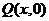 的速度为常数,因此
的速度为常数,因此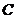 是错误的,故选
是错误的,故选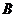 .
.
12. 设过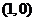 的直线与
的直线与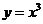 相切于点
相切于点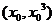 ,所以切线方程为
,所以切线方程为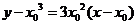
即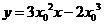 ,又
,又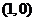 在切线上,则
在切线上,则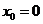 或
或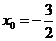 ,
,
当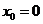 时,由
时,由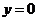 与
与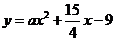 相切可得
相切可得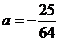 ,
,
当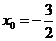 时,由
时,由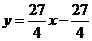 与
与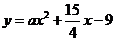 相切可得
相切可得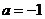 ,所以选
,所以选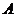 .
.
二、填空题:本大题共4小题,每小题4分,共16分。
13.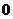 14.
14.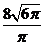
 15.
15.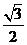 16. ABC
16. ABC
13..因为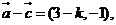 所以
所以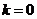 .
.
14.设球的半径为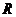 ,依题设有
,依题设有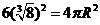 ,则
,则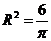 ,球的体积为
,球的体积为
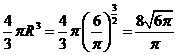
15.由数形结合,半圆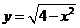 在直线
在直线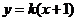 之下必须
之下必须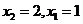 ,则直线
,则直线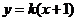 过点
过点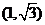 ,则
,则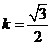

16. 因为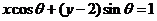 所以点
所以点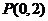 到
到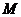 中每条直线的距离
中每条直线的距离
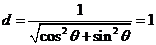
即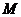 为圆
为圆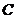 :
: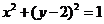 的全体切线组成的集合,所以存在圆心在
的全体切线组成的集合,所以存在圆心在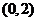 ,半径大于1的圆与
,半径大于1的圆与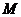 中所有直线相交, 也存在圆心在
中所有直线相交, 也存在圆心在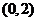 ,半径小于1的圆与
,半径小于1的圆与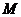 中所有直线均不相交, 也存在圆心在
中所有直线均不相交, 也存在圆心在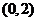 ,半径等于1的圆与
,半径等于1的圆与 中所有直线相切,
中所有直线相切,
故ABC正确,
又因 中的边能组成两类大小不同的正三角形,故D错误,
中的边能组成两类大小不同的正三角形,故D错误,
故命题中正确的序号是ABC
三、解答题:本大题共6小题,共74分。
17.解:(1)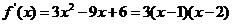 ,
,
因为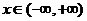 ,
,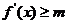 , 即
, 即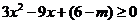 恒成立,
恒成立,
所以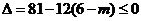 , 得
, 得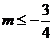 ,即
,即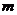 的最大值为
的最大值为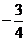
(2) 因为 当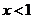 时,
时,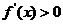 ;当
;当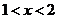 时,
时,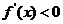 ;当
;当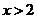 时,
时,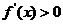 ;
;
所以 当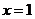 时,
时,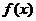 取极大值
取极大值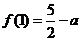 ;
;
当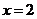 时,
时,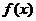 取极小值
取极小值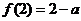 ;
;
故当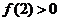 或
或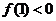 时, 方程
时, 方程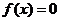 仅有一个实根. 解得
仅有一个实根. 解得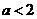 或
或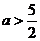 .
.
18.解:(1)设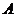 表示资助总额为零这个事件,则
表示资助总额为零这个事件,则
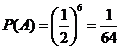
(2)设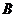 表示资助总额超过15万元这个事件,则
表示资助总额超过15万元这个事件,则