19.解:(1)由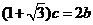 得
得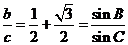
则有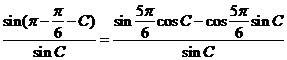 =
=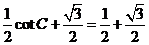
得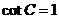 即
即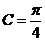 .
.
(2) 由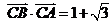 推出
推出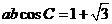 ;而
;而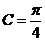 ,
,
即得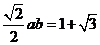 ,
,
则有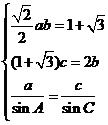 解得
解得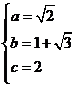 .
.
20.解:方法(一):
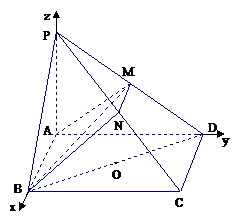
(1)证:依题设,M在以BD为直径的球面上,则BM⊥PD.
因为PA⊥平面ABCD,则PA⊥AB,又AB⊥AD,
所以AB⊥平面PAD,则AB⊥PD,因此有PD⊥平面ABM,所以平面ABM⊥平面PCD.
(2)设平面ABM与PC交于点N,因为AB∥CD,所以AB∥平面PCD,则AB∥MN∥CD,
由(1)知,PD⊥平面ABM,则MN是PN在平面ABM上的射影,
所以 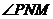 就是
就是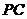 与平面
与平面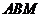 所成的角,
所成的角,
且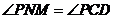
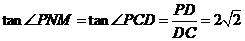


所求角为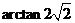
(3)因为O是BD的中点,则O点到平面ABM的距离等于D点到平面ABM距离的一半,由(1)知,PD⊥平面ABM于M,则|DM|就是D点到平面ABM距离.
因为在Rt△PAD中,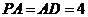 ,
,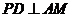 ,所以
,所以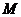 为
为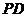 中点,
中点,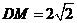 ,则O点到平面ABM的距离等于
,则O点到平面ABM的距离等于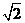 。
。
方法二:
(1)同方法一;
(2)如图所示,建立空间直角坐标系,则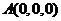 ,
,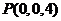 ,
,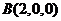 ,
,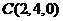 ,
,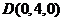 ,
,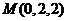 ,
,
设平面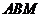 的一个法向量
的一个法向量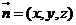 ,由
,由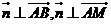 可得:
可得: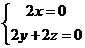 ,令
,令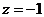 ,则
,则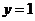 ,即
,即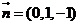 .设所求角为
.设所求角为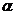 ,则
,则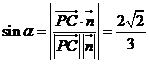 ,
,
所求角的大小为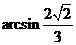 .
.
(3)设所求距离为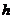 ,由
,由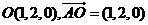 ,得:
,得: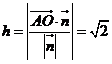
21. 解: (1) 由于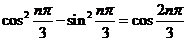 ,故
,故
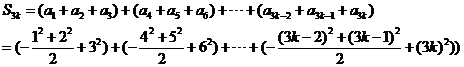
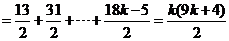 ,
,
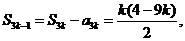
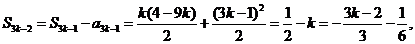
故 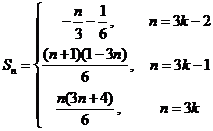 (
(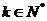 )
)
(2)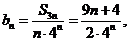
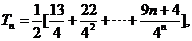

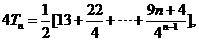
两式相减得
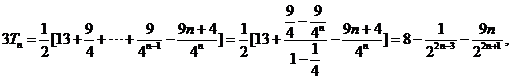
故 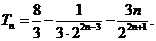
22.解: (1)设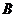
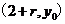 ,过圆心
,过圆心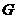 作
作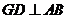 于
于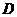 ,
,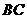 交长轴于
交长轴于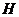
由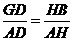 得
得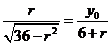 ,
,
即 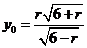 (1)
(1)
而点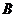
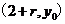 在椭圆上,
在椭圆上,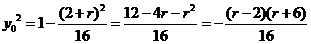 (2)
(2)
由(1)、 (2)式得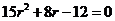 ,解得
,解得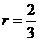 或
或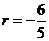 (舍去)
(舍去)
(2) 设过点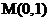 与圆
与圆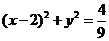 相切的直线方程为:
相切的直线方程为: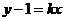 (3)
(3)
则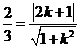 ,即
,即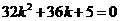 (4)
(4)
解得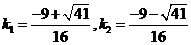
将(3)代入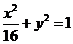 得
得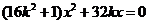 ,则异于零的解为
,则异于零的解为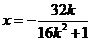
设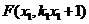 ,
,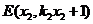 ,则
,则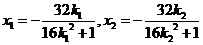
则直线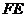 的斜率为:
的斜率为: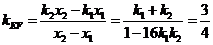
于是直线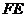 的方程为:
的方程为: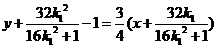
即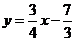
则圆心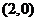 到直线
到直线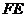 的距离
的距离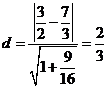
故结论成立.












