第Ⅱ卷
本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须回答。第22题~第24题为选考题,考生根据要求做答。
二.填空题:本大题共4小题,每小题5分。
(13)已知a与b为两个不共线的单位向量,k为实数,若向量a+b与向量ka-b垂直,则k= _____。
解析:本题考查向量的基本运算和性质,属于容易题。
解法一:直接法 (a+b)(ka-b)=0展开易得k=1.
解法二:凭经验 k=1时a+b, a-b数量积为0,易知k=1.
(14)若变量x,y满足约束条件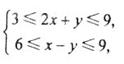 则z=x+2y的最小值为___________。
则z=x+2y的最小值为___________。
解析:本题考查线性规划的基本知识,属于容易题。只需画出线性区域即可。易得z=x+2y的最小值为-6。
(15)△ABC中B=120°,AC=7,AB=5,则△ABC的面积为__________。
解析:本题考查余弦定理和面积公式,属于容易题。
有余弦定理得
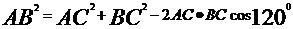
所以BC=3,有面积公式得S=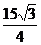
(16)已知两个圆锥有公共底面,且两个圆锥的顶点和底面的圆周都在同一个球面上,若圆锥底面面积是这个球面面积的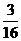 ,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为__________。
,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为__________。
解析:本题考查球内接圆锥问题,属于较难的题目。
由圆锥底面面积是这个球面面积的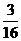
得 所以
所以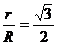 ,则小圆锥的高为
,则小圆锥的高为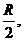 大圆锥的高为
大圆锥的高为 ,所以比值为
,所以比值为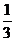
三、解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)
已知等比数列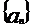 中,
中, ,公比
,公比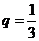 。
。
(I)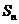 为
为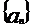 的前
的前 项和,证明:
项和,证明:
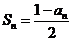
(II)设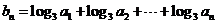 ,求数列
,求数列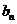 的通项公式。
的通项公式。
解析:本题考查等比数列基本知识和等差数列的基本知识。
(I)


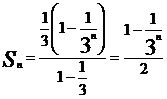

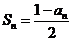
(II)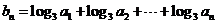
=-(1+2+3+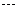
 +n)=-
+n)=-
 数列
数列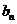 的通项公式为
的通项公式为 =-
=-
(18)(本小题满分12分)
如图,四棱锥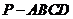 中,底面
中,底面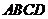 为平行四边形。
为平行四边形。 底面
底面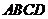 。
。
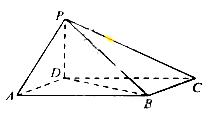
(I)证明: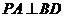
(II)设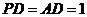 ,求棱锥
,求棱锥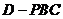 的高。
的高。
解:(Ⅰ )因为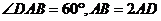 , 由余弦定理得
, 由余弦定理得
从而BD2+AD2= AB2,故BD AD
AD
又PD 底面ABCD,可得BD
底面ABCD,可得BD PD
PD
所以BD 平面PAD. 故PA
平面PAD. 故PA BD
BD
(Ⅱ)过D作DE⊥PB于E,由(I)知BC⊥BD,又PD⊥底面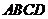 ,所以BC⊥平面PBD,而DE
,所以BC⊥平面PBD,而DE 平面PBD,故DE⊥BC,所以DE⊥平面PBC
平面PBD,故DE⊥BC,所以DE⊥平面PBC
由题设知PD=1,则BD=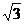 ,PB=2,
,PB=2,
由DE﹒PB=PD﹒BD得DE= ,即棱锥
,即棱锥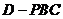 的高为
的高为












