19 (本小题满分12分)
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下:
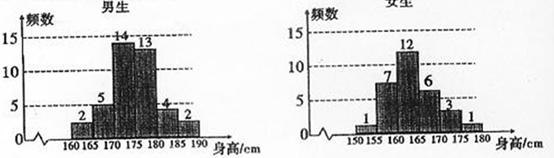
(Ⅰ)估计该校男生的人数;
(Ⅱ)估计 该校学生身高在170~185cm之间的概率;
该校学生身高在170~185cm之间的概率;
(Ⅲ)从样 本中
本中 身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率.
身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率.
【命题意图】本题主要考查统计里面的分层抽样,及古典型概率问题.
【参考答案】解 :(Ⅰ)样本中男生人数为40 ,由分层抽样比例为10%估计全校男生人数为400.
(Ⅱ)由统计图知,样本中身高在170~185cm之间的学生有14+13+4+3+1=35人,样本容量为70 ,所以样本中学生身高在170~185cm之间的频率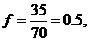 故有
故有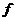 估计该校学生身高在170~180cm之间的概率
估计该校学生身高在170~180cm之间的概率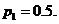
(Ⅲ)样本中身高在180~185cm之间的男生有4人,设其编号为①,②,③,④,
 样本中身高在185~190cm之间的男生有2人,设其编号为⑤,⑥,
样本中身高在185~190cm之间的男生有2人,设其编号为⑤,⑥,
从上述6人中任取2人的树状图为:

故从样本中身高在180~190cm之间的男生中任选2人的所有可能结果数为15,至少有1人身高在185~190cm之间的可能结果数为9,因此,所求概率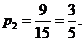
【点评】本题是我们平时统计里常考的题,只要概念掌握的好,前两问很容易得满分,第三问就要我们能够熟练运用树状图表示基本事件了,这样即要求不重也不能漏,需要考生做题细心.
20.(本小题满分13分)
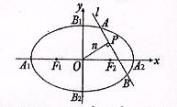
如图,椭圆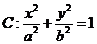 的顶点为
的顶点为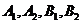 ,焦点为
,焦点为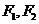 ,
,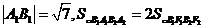 .
.
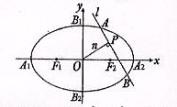
(Ⅰ)求椭圆C的方程;
(Ⅱ)设n 为过原点的直线,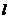 是与n垂直相交于P点,与椭圆相交于A, B两点的直线,
是与n垂直相交于P点,与椭圆相交于A, B两点的直线,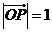 .是否存在上述直线
.是否存在上述直线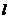 使
使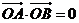 成立?若存在,求出直线
成立?若存在,求出直线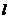 的方程;并说出;若不存在,请说明理由.
的方程;并说出;若不存在,请说明理由.
【命题意图】本题主要考查圆锥曲线,以及运用代数的思想来解决椭圆和直线之间的一些几何问题,让考生充分体会解析几何的本质,也考查考生做题的仔细程度.
【参考答案】解 : (Ⅰ)由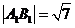 知a2+b2=7, ①
知a2+b2=7, ①
又b2=a2-c2 ③
由 ①,②,③解得a 2=4,b2=3,
2=4,b2=3,
故椭圆C的方程为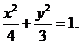
(Ⅱ) 设A,B两点的坐标分别为 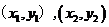
假设使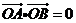 成立的直线l存在,
成立的直线l存在,
(i) 当l不垂直于x轴时,设l的方程为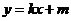 ,
,
由l与n垂直相交于P点且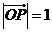 得
得

【点评】本题主要对圆锥曲线中的椭圆进行了考查,问题的设置上比较简单,但第二问运算量大,学生不易得分,是一道即考查 学生基础知识又考查运算,分析能力的题.
学生基础知识又考查运算,分析能力的题.
21、(本小题满分14分)
已知函数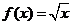 ,
,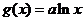 ,
,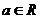 .
.
(Ⅰ)若曲线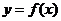 与曲线
与曲线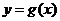 相交,且在交点处有相同的切线,求
相交,且在交点处有相同的切线,求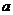 的值及该切线的方程;
的值及该切线的方程;
(Ⅱ)设函数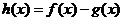 ,当
,当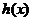 存在最小值时,求其最小值
存在最小值时,求其最小值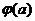 的解析式;
的解析式;
(Ⅲ)对(Ⅱ)中的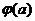 ,证明:当
,证明:当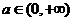 时,
时, 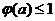 .
.

(ii)当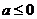 时,
时,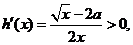
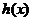 在(0,+∞)上递增,无最小值。
在(0,+∞)上递增,无最小值。
故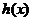 的最小值
的最小值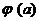 的解析式为
的解析式为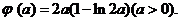
(Ⅲ)由(Ⅱ)知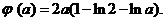
则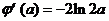 ,令
,令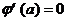 解得
解得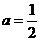 .
.
当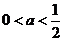 时,
时,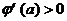 ,∴
,∴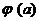 在
在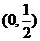 上递增;
上递增;
当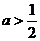 时,
时,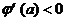 ,∴
,∴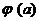 在
在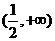 上递减.
上递减.
∴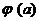 在
在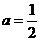 处取得最大值
处取得最大值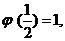
∵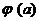 在
在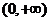 上有且只有一个极值点,所以
上有且只有一个极值点,所以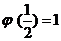 也是
也是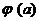 的最大值.
的最大值.
∴当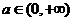 时,总有
时,总有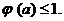
【点评】本题题目条件给的比较清晰,直接.只要抓住概念就可以很好的解决第一问,后两问主要难在需要细心并且有耐心的去分类讨论,运算,方法并不难,所以考试时做这一类题时力争拿到第一步分,后面的尽量争取.



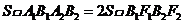 知a=2c, ②
知a=2c, ②








