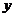第I卷(选择题 共60分)
一.选择题
1.复数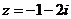 (
(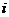 为虚数单位)在复平面内对应的点位于( )
为虚数单位)在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】C
【解析】本题考查的知识点是复数的几何意义.由几何意义可知复数在第三象限.
2.设点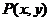 ,则“
,则“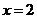 且
且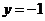 ”是“点
”是“点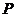 在直线
在直线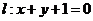 上”的( )
上”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】A
【解析】本题考查的知识点是逻辑中充要条件的判定.因为 点代入直线方程,符合方程,即“
点代入直线方程,符合方程,即“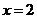 且
且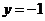 ”可推出“点
”可推出“点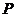 在直线
在直线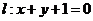 上”;而点
上”;而点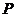 在直线上,不一定就是
在直线上,不一定就是 点,即“点
点,即“点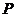 在直线
在直线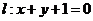 上”推不出“
上”推不出“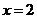 且
且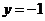 ”.故“
”.故“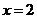 且
且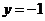 ”是“点
”是“点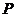 在直线
在直线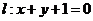 上”的充分而不必要条件.
上”的充分而不必要条件.
3.若集合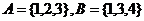 ,则
,则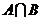 的子集个数为( )
的子集个数为( )
A.2 B.3 C.4 D.16
【答案】C
【解析】本题考查的是集合的交集和子集.因为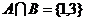 ,有2个元素,所以子集个数为
,有2个元素,所以子集个数为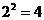 个.
个.
4.双曲线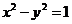 的顶点到其渐近线的距离等于( )
的顶点到其渐近线的距离等于( )
A.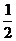 B.
B.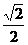 C.1 D.
C.1 D.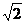
【答案】B
【解析】本题考查的是双曲线的性质.因为双曲线的两个顶点到两条渐近线的距离都相等,故可取双曲线的一个顶点为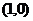 ,取一条渐近线为
,取一条渐近线为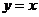 ,所以点
,所以点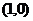 到直线
到直线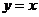 的距离为
的距离为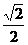 .
.
5.函数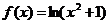 的图象大致是( )
的图象大致是( )

A. B. C. D.
【答案】A
【解析】本题考查的是对数函数的图象.由函数解析式可知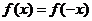 ,即函数为偶函数,排除C;由函数过
,即函数为偶函数,排除C;由函数过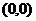 点,排除B,D.
点,排除B,D.
6.若变量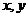 满足约束条件
满足约束条件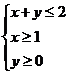 ,则
,则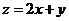 的最大值和最小值分别为( )
的最大值和最小值分别为( )
A.4和3 B.4和2 C.3和2 D.2和0
【答案】B
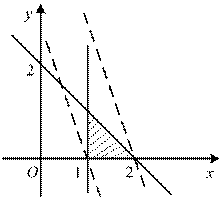
【解析】本题考查的简单线性规划.如图,可知目标函数最大值和最小值分别为4和2.
7.若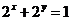 ,则
,则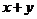 的取值范围是( )
的取值范围是( )
A.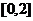 B.
B.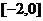 C.
C.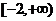 D.
D.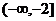
【答案】D
【解析】本题考查的是均值不等式.因为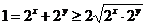 ,即
,即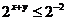 ,所以
,所以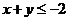 ,当且仅当
,当且仅当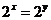 ,即
,即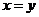 时取等号.
时取等号.
8.阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数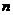 后,输出的
后,输出的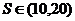 ,那么
,那么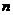 的值为( )
的值为( )
A.3 B.4 C.5 D.6
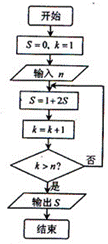
【答案】B
【解析】本题考查的是程序框图.循环前: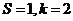 ;第1次判断后循环:
;第1次判断后循环: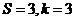 ;第2次判断后循环:
;第2次判断后循环: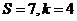 ;第3次判断后循环:
;第3次判断后循环: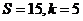 .故
.故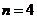 .
.
9.将函数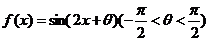 的图象向右平移
的图象向右平移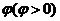 个单位长度后得到函数
个单位长度后得到函数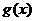 的图象,若
的图象,若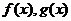 的图象都经过点
的图象都经过点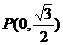 ,则
,则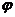 的值可以是( )
的值可以是( )
A.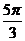 B.
B.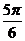 C.
C.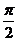 D.
D.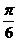
【答案】B
【解析】本题考查的三角函数的图像的平移.把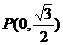 代入
代入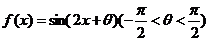 ,解得
,解得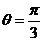 ,所以
,所以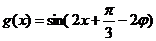 ,把
,把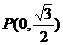 代入得,
代入得,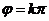 或
或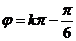 ,观察选项,故选B
,观察选项,故选B
10.在四边形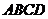 中,
中,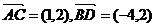 ,则该四边形的面积为( )
,则该四边形的面积为( )
A.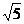 B.
B.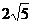 C.5 D.10
C.5 D.10
【答案】C
【解析】本题考查的是向量垂直的判断以及向量的模长.因为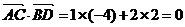 ,所以
,所以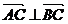 ,所以四边形的面积为
,所以四边形的面积为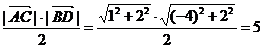 ,故选C
,故选C
11.已知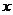 与
与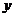 之间的几组数据如下表:
之间的几组数据如下表:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 2 | 1 | 3 | 3 | 4 |
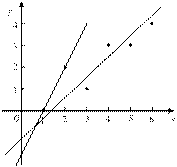
假设根据上表数据所得线性回归直线方程为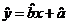 .若某同学根据上表中前两组数据
.若某同学根据上表中前两组数据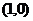 和
和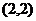 求得的直线方程为
求得的直线方程为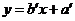 ,则以下结论正确的是( )
,则以下结论正确的是( )
A.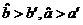 B.
B.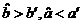 C.
C.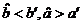 D.
D.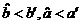
【答案】C
【解析】本题考查的是线性回归方程.画出散点图,可大致的画出两条直线(如下图),由两条直线的相对位置关系可判断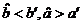 .故选C
.故选C
12.设函数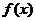 的定义域为
的定义域为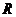 ,
,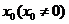 是
是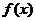 的极大值点,以下结论一定正确的是( )
的极大值点,以下结论一定正确的是( )
A.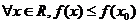 B.
B.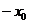 是
是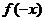 的极小值点
的极小值点
C.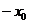 是
是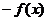 的极小值点 D.
的极小值点 D.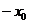 是
是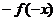 的极小值点
的极小值点
【答案】D
【解析】本题考查的是函数的极值.函数的极值不是最值,A错误;因为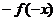 和
和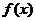 关于原点对称,故
关于原点对称,故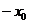 是
是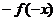 的极小值点,D正确.
的极小值点,D正确.
二.填空题
13.已知函数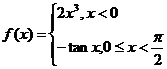 ,则
,则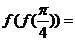
【答案】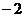
【解析】本题考查的是分段函数求值.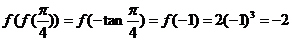 .
.
14.利用计算机产生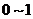 之间的均匀随机数
之间的均匀随机数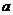 ,则事件“
,则事件“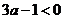 ”发生的概率为
”发生的概率为
【答案】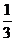
【解析】本题考查的是几何概型求概率.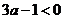 ,即
,即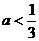 ,所以
,所以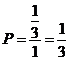 .
.
15.椭圆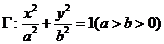 的左、右焦点分别为
的左、右焦点分别为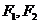 ,焦距为
,焦距为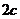 .若直线
.若直线 与
与
椭圆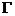 的一个交点
的一个交点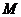 满足
满足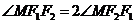 ,则该椭圆的离心率等于
,则该椭圆的离心率等于
【答案】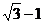
【解析】本题考查的是圆锥曲线的离心率.由题意可知,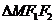 中,
中,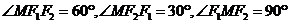 ,所以有
,所以有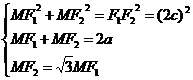 ,整理得
,整理得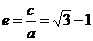 ,故答案为
,故答案为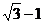 .
.
16.设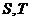 是
是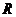 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从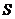 到
到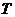 的函数
的函数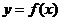 满足;
满足;
(i)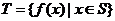 ;(ii)对任意
;(ii)对任意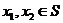 ,当
,当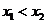 时,恒有
时,恒有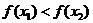 .
.
那么称这两个集合“保序同构”.现给出以下3对集合:
①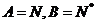 ;
;
②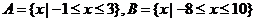 ;
;
③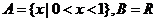 .
.
其中,“保序同构”的集合对的序号是 (写出所有“保序同构”的集合对的序号)
【答案】①②③
【解析】本题考查的函数的性质.由题意可知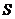 为函数的一个定义域,
为函数的一个定义域,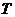 为其所对应的值域,且函数
为其所对应的值域,且函数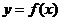 为单调递增函数.对于集合对①,可取函数
为单调递增函数.对于集合对①,可取函数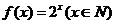 ,是“保序同构”;对于集合对②,可取函数
,是“保序同构”;对于集合对②,可取函数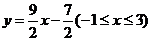 ,是“保序同构”;对于集合对③,可取函数
,是“保序同构”;对于集合对③,可取函数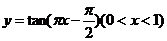 ,是“保序同构”.故答案为①②③.
,是“保序同构”.故答案为①②③.