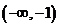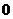20.(本小题满分12分)如图,在抛物线 的焦点为
的焦点为 ,准线
,准线 与
与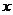 轴的交点为
轴的交点为 .点
.点 在抛物线
在抛物线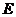 上,以
上,以 为圆心
为圆心 为半径作圆,设圆
为半径作圆,设圆 与准线
与准线 的交于不同的两点
的交于不同的两点 .
.
(1)若点 的纵坐标为2,求
的纵坐标为2,求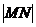 ;
;
(2)若 ,求圆
,求圆 的半径.
的半径.

本小题主要考查抛物线的方程、圆的方程与性质、直线与圆的位置关系等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想.满分12分.
解:(Ⅰ)抛物线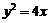 的准线
的准线 的方程为
的方程为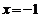 ,
,
由点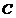 的纵坐标为
的纵坐标为 ,得点
,得点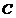 的坐标为
的坐标为
所以点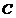 到准线
到准线 的距离
的距离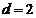 ,又
,又 .
.
所以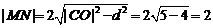 .
.
(Ⅱ)设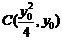 ,则圆
,则圆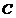 的方程为
的方程为 ,
,
即 .
.
由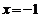 ,得
,得
设 ,
,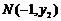 ,则:
,则:

由 ,得
,得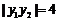
所以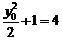 ,解得
,解得 ,此时
,此时
所以圆心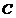 的坐标为
的坐标为 或
或
从而 ,
, ,即圆
,即圆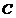 的半径为
的半径为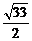
21(本小题满分12分)如图,在等腰直角三角形 中,
中,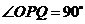 ,
, ,点
,点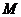 在线段
在线段 上.
上.
(1)若 ,求
,求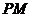 的长;
的长;
(2)若点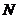 在线段
在线段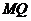 上,且
上,且 ,问:当
,问:当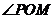 取何值时,
取何值时, 的面积最小?并求出面积的最小
的面积最小?并求出面积的最小
值.

本小题主要考查解三角形、同角三角函数的基本关系、两角和与差的三角函数等基础知识,考查推理论证能力、抽象概括能力、运算求解能力,考查函数与方程思想、数形结合思想、化归与转化思想.满分12分.
解:(Ⅰ)在 中,
中, ,
, ,
, ,
,
由余弦定理得, ,
,
得 ,
,
解得 或
或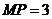 .
.
(Ⅱ)设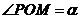 ,
, ,
,
在 中,由正弦定理,得
中,由正弦定理,得 ,
,
所以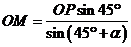 ,
,
同理
故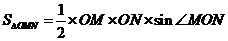
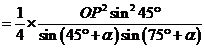

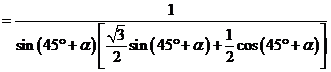
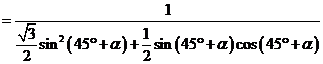



因为 ,
, ,所以当
,所以当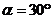 时,
时, 的最大值为
的最大值为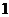 ,此时
,此时 的面积取到最小值.即2
的面积取到最小值.即2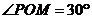 时,
时, 的面积的最小值为
的面积的最小值为 .
.
22(本小题满分14分)已知函数 (
( ,
, 为自然对数的底数).
为自然对数的底数).
(1)若曲线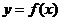 在点
在点 处的切线平行于
处的切线平行于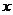 轴,求
轴,求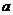 的值;
的值;
(2)求函数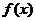 的极值;
的极值;
(3)当 的值时,若直线
的值时,若直线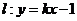 与曲线
与曲线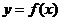 没有公共点,求
没有公共点,求 的最大值.
的最大值.
本小题主要考查函数与导数,函数的单调性、极值、零点等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、数形结合思想、分类与整合思想、化归与转化思想.满分14分.
解:(Ⅰ)由 ,得
,得 .
.
又曲线 在点
在点 处的切线平行于
处的切线平行于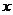 轴,
轴,
得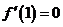 ,即
,即 ,解得
,解得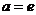 .
.
(Ⅱ) ,
,
①当 时,
时, ,
, 为
为 上的增函数,所以函数
上的增函数,所以函数 无极值.
无极值.
②当 时,令
时,令 ,得
,得 ,
,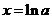 .
.
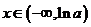 ,
,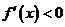 ;
; ,
, .
.
所以 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
故 在
在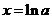 处取得极小值,且极小值为
处取得极小值,且极小值为 ,无极大值.
,无极大值.
综上,当 时,函数
时,函数 无极小值;
无极小值;
当 ,
, 在
在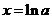 处取得极小值
处取得极小值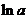 ,无极大值.
,无极大值.
(Ⅲ)当 时,
时,
令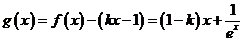 ,
,
则直线 :
: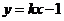 与曲线
与曲线 没有公共点,
没有公共点,
等价于方程 在
在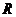 上没有实数解.
上没有实数解.
假设 ,此时
,此时 ,
,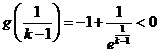 ,
,
又函数 的图象连续不断,由零点存在定理,可知
的图象连续不断,由零点存在定理,可知 在
在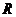 上至少有一解,与“方程
上至少有一解,与“方程 在
在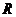 上没有实数解”矛盾,故
上没有实数解”矛盾,故 .
.
又 时,
时, ,知方程
,知方程 在
在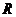 上没有实数解.
上没有实数解.
所以 的最大值为
的最大值为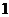 .
.
解法二:
(Ⅰ)(Ⅱ)同解法一.
(Ⅲ)当 时,
时, .
.
直线 :
: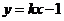 与曲线
与曲线 没有公共点,
没有公共点,
等价于关于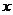 的方程
的方程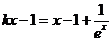 在
在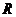 上没有实数解,即关于
上没有实数解,即关于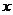 的方程:
的方程:
 (*)
(*)
在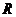 上没有实数解.
上没有实数解.
①当 时,方程(*)可化为
时,方程(*)可化为 ,在
,在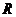 上没有实数解.
上没有实数解.
②当 时,方程(*)化为
时,方程(*)化为 .
.
令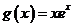 ,则有
,则有 .
.
令 ,得
,得 ,
,
当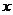 变化时,
变化时,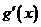 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
当 时,
时, ,同时当
,同时当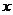 趋于
趋于 时,
时, 趋于
趋于 ,
,
从而 的取值范围为
的取值范围为 .
.
所以当 时,方程(*)无实数解,
时,方程(*)无实数解,
解得 的取值范围是
的取值范围是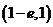 .
.
综上,得 的最大值为
的最大值为 .
.