山东理数答案
一.选择题
1.C 2.B 3.D 4.D 5.C 6.D 7.A 8.B 9.C 10.A 11.A 12.B
二.填空题
13.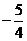 14.
14.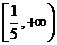 15.
15.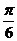 16.
16.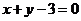
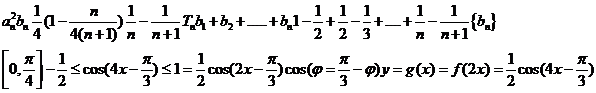
三.解答题

(Ⅱ)由(Ⅰ)知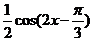 ,将函数
,将函数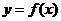 的图
的图 像上各点的横坐标缩短到原来的
像上各点的横坐标缩短到原来的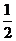 ,纵坐标
,纵坐标 不变,得到函数
不变,得到函数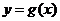 的图象,可知
的图象,可知
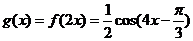
因为 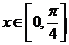 ,
,
所以 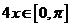 ,
,
因此 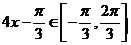 ,
,
故 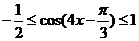 。
。
所以 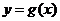 在
在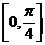 上的最大值和最小值分别为
上的最大值和最小值分别为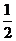 和
和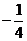 .
.
(18)本小题主要考查等差数列的基本知识,考查逻辑推理、等价变形和运算能力。
解:(Ⅰ) 设等差数列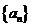 的首项为
的首项为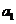 ,公差为d
,公差为d

所以数列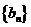 的前n项和
的前n项和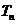 =
=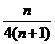
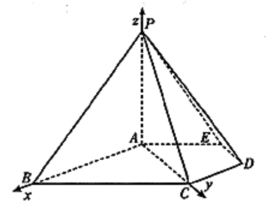
(19)本小题主要考察空间中的基本关系,考察线面垂直、面面垂直的判定以及线面角和集合体体积的计算,考查识图能力、空间想象力和逻辑推理能力,满分12分
(|)证明:
在△ABC中,因为∠ABC=45°,BC=4,AB=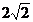 ,
,
所以AC2=AB+BC2 -2AB·BC·cos45°=8
-2AB·BC·cos45°=8
因此 AC=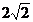 ,
,
故BC2=AC2+AB2,
所以∠BAC=90°----------------------------------------------------
又PA⊥平面ABCDE,AB∥CD,
所以CD⊥PA,CD⊥AC,
又 PA,AC 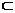 平面PAC,且PA
平面PAC,且PA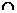 AC
AC =A,
=A,
所以 CD⊥PAC,又 CD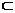 平面PCD,
平面PCD,
所以 平面PCD⊥平面PAC--------------------------------------------

则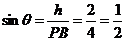 ,
,
又 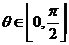 ,
,
所以 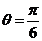
解法二:
由(|)知AB,AC,AP两两相互垂直,分别以AB、AC、AP为x轴、y轴、z轴建立如图所示的空间直角坐标系,由于△PAB是等腰三角形,
 所以 PA=AB=
所以 PA=AB=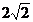 ,
,
又AC=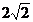 ,
,

所以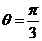 ,
,
因此直线 PB与平面PCD所成的角为
PB与平面PCD所成的角为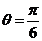
(Ⅲ)因为AC∥ED,CD⊥AC,
所以 四边形ACDE是直角梯形,
因为 AE=2,∠ABC=45°,AE∥BC,
所以 ∠BAE=135°,
因此 ∠CAE=45°,
故 CD=AE·sin45°==2×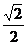 =
=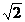 ,
,
所以 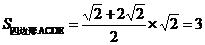
又 PA⊥平面ABCDE,
所以