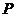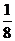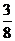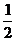(20)本小题主要考查离散型随机变量的分布列和数学期望,考查对立事件、独立事件的概率和求解方法,考查用概率知识解决实际问题的能力.
解:设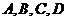 分别为第一、二、三、四个问题.用
分别为第一、二、三、四个问题.用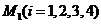 表示甲同学第
表示甲同学第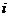 个问题回答正确,用
个问题回答正确,用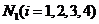 表示甲同学第
表示甲同学第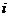 个问题回答错误,则
个问题回答错误,则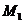 与
与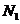 是对立事件
是对立事件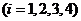 .由题意得
.由题意得
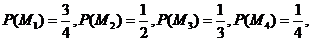
所以
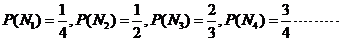
(Ⅰ)记“甲同学能进入下一轮”为事件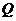 ,
,
则
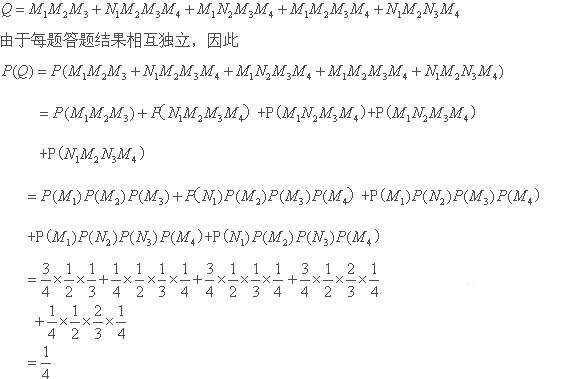
(Ⅱ)由题意,随机变量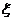 的可能取值为:
的可能取值为: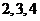 .
.
由于每题答题结果相互独立,
所以
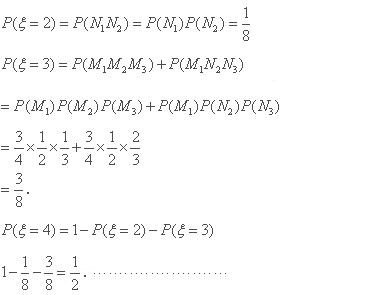
因此 随机变量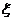 的分布列为
的分布列为
|
|
|
|
|
|
|
|
所以
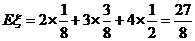 .
.
(21)本小题主要考查椭圆、双曲线的基本概念和基本性质。考查直线和椭圆的位置关系,考查坐标化、定值和存在性问题,考查数行结合思想和探求问题的能力。
解(Ⅰ)设椭圆的半焦距为c,由题意知: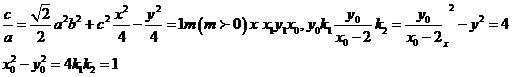
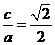 ,2a+2c=4(
,2a+2c=4(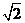 +1)
+1)
所以a=2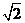 ,c=2,
,c=2,
又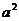 =
=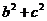 ,因此b=2。
,因此b=2。
故 椭圆的标准方程为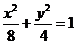
由题意设等轴双曲线的标准方程为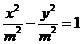
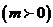 ,因为等轴双曲线的顶点是椭圆的焦点。
,因为等轴双曲线的顶点是椭圆的焦点。
所以m=2,
因此 双曲线的标准方程为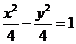
(Ⅱ)设A(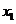 ,
,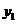 ),B(
),B(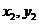 ),P(
),P(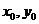 ),
),
则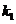 =
=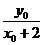 ,
,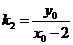 。
。
因为点P在双曲线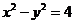 上,所以
上,所以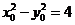 。
。
因此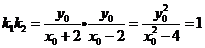 ,
,
即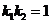

同理可 得
得
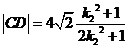 .
.
则 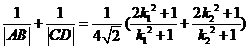 ,
,
又 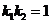 ,
,
所以 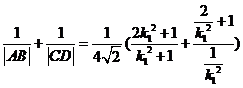
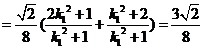 .
.
故 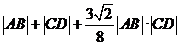
因此 存在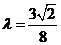 ,使
,使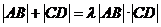 恒成立.
恒成立.
(22)本小题主要考查导数的概念以及利用导数研究函数性质的能力,考查分类讨论思想、数形结合思想、等价变换思想,以及综合运用知识解决新情境、新问题的能力。
解:(Ⅰ)因为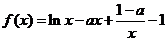 ,
,
所以 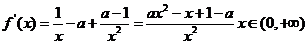 ,
,
令 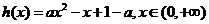 ,
,

①当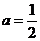 时,
时,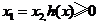 恒成立,此时
恒成立,此时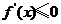 ,函数
,函数  在
在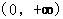 上单调递减;
上单调递减;
②当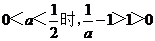 ,
,
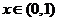 时,
时,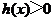 ,此时
,此时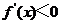 ,函数
,函数 单调递减;
单调递减;
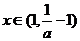 时
时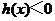 ,此时
,此时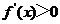 ,函数
,函数  单调递增;
单调递增;
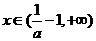 时,
时,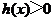 ,此时
,此时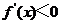 ,函数
,函数 单调递减;
单调递减;
③当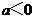 时,由于
时,由于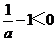 ,
,
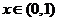 ,
,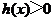 ,此时
,此时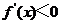 ,函数
,函数  单调递减;
单调递减;
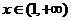 时,
时,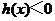 ,此时
,此时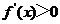 ,函数
,函数 单调递增.
单调递增.
综上所述:

(Ⅱ)因为a=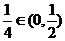 ,由(Ⅰ)知,
,由(Ⅰ)知,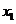 =1,
=1,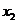 =3
=3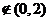 ,当
,当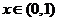 时,
时,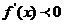 ,函数
,函数 单调递减;
单调递减;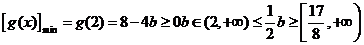 当
当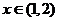 时,
时,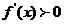 ,函数
,函数 单调递增,所以
单调递增,所以 在(0,2)上的最小值为
在(0,2)上的最小值为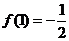 。
。
由于“对任意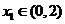 ,存在
,存在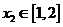 ,使
,使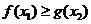 ”等价于
”等价于
“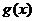 在
在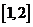 上的最小值不大于
上的最小值不大于 在(0,2)上的最小值
在(0,2)上的最小值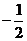 ”(*)
”(*)
又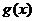 =
=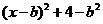 ,
,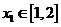 ,所以
,所以
①当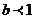 时,因为
时,因为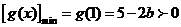 ,此时与(*)矛盾
,此时与(*)矛盾
②当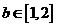 时,因为
时,因为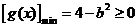 ,同样与(*)矛盾
,同样与(*)矛盾
③当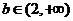 时,因为
时,因为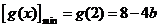 ,解不等式8-4b
,解不等式8-4b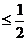 ,可得
,可得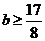
综上,b的取值范围是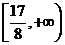 。
。