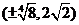三、解答题,共72分。解答应写出文字说明、证明过程或演算步骤。
(18)(本题满分14分)已知函数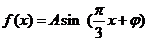 ,
,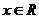 ,
,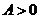 ,
,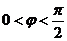 .
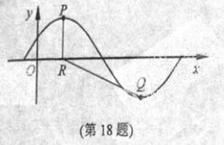
.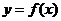 的部分图像,如图所示,
的部分图像,如图所示,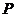 、
、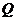 分别为该图像的最高点和最低点,点
分别为该图像的最高点和最低点,点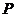 的坐标为
的坐标为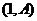 .
.
(Ⅰ)求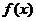 的最小正周期及
的最小正周期及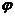 的值;(Ⅱ)若点
的值;(Ⅱ)若点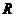 的坐标为
的坐标为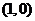 ,
,
19(本题满分14分)已知公差不为0的等差数列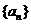 的首项
的首项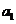 为
为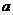 (
(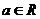 ),且
),且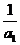 ,
,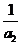 ,
,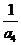 成等比数列(Ⅰ)求数列
成等比数列(Ⅰ)求数列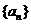 的通项公式(Ⅱ)对
的通项公式(Ⅱ)对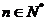 ,试比较
,试比较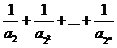 与
与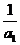 的大小.
的大小.
【解析】:(Ⅰ)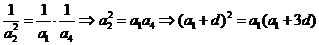
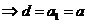
数列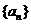 的通项公式
的通项公式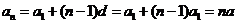
(Ⅱ)记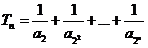 因为
因为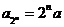 ,所以
,所以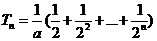
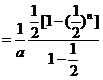
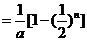 从而当
从而当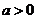 时,
时,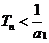 ;当
;当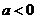 时,
时,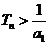
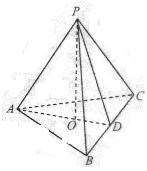
(20)(本题满分14分)如图,在三棱锥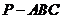 中,
中,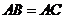 ,
,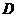 为
为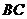 的
的 中点,
中点,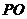 ⊥平面
⊥平面 ,垂足
,垂足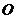 落在线段
落在线段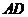 上.
上.
(Ⅰ)证明: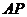 ⊥
⊥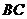 ;(Ⅱ)已知
;(Ⅱ)已知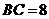 ,
,
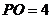 ,
,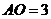 ,
,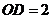 .求二面角
.求二面角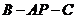 的大小.
的大小.
【解析】::(Ⅰ)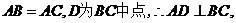

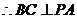
(Ⅱ)在平面 内作
内作
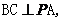 得
得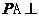 平面
平面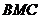 ,所以
,所以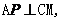
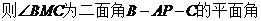 ,
,
在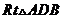 中,
中,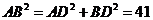 得
得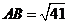
在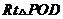 中,
中,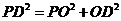 ,
,
在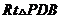 中,
中,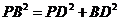
所以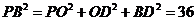 得
得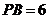 ,
,
在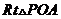 中,
中,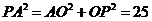 得
得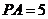
又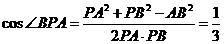 从而
从而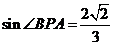 故
故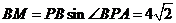
同理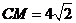 ,因为
,因为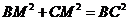 所以
所以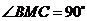 即二面角
即二面角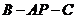 的大小为
的大小为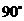
21(本题满分15分)设函数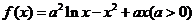 (Ⅰ)求
(Ⅰ)求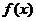 单调区间(Ⅱ)求所有实数
单调区间(Ⅱ)求所有实数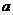 ,使
,使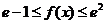 对
对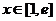 恒成立
恒成立
注: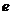 为自然对数的底数
为自然对数的底数
【解析】:(Ⅰ)因为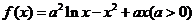 所以
所以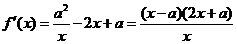 由于
由于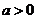
所以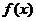 的增区间为
的增区间为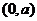 ,减区间为
,减区间为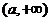 。
。
(Ⅱ)由题意得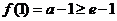 即
即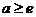 。由(Ⅰ)知
。由(Ⅰ)知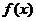 在
在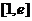 单调递增,要使
单调递增,要使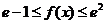
对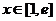 恒成立,只要
恒成立,只要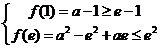 解得
解得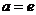
22.(本题满分15分)如图,设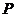 是抛物线
是抛物线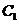 :
: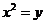 上动点。圆
上动点。圆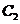 :
: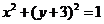 的圆心为点M,过点
的圆心为点M,过点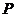 做圆
做圆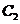 的两条切线,交直线
的两条切线,交直线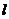 :
: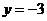 于
于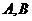 两点。
两点。
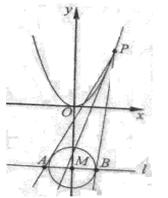
(Ⅰ)求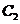 的圆心
的圆心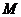 到抛物线
到抛物线 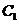 准线的距离。
准线的距离。
(Ⅱ)是否存在点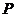 ,使线段
,使线段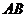 被抛物线
被抛物线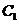 在点
在点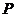 处得切线平分,若存在,求出点
处得切线平分,若存在,求出点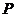 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
【解析】:(Ⅰ)由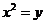 得准
得准 线方程为
线方程为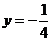 ,由
,由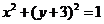 得
得 又
又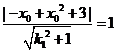 即
即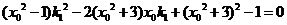
同理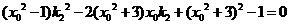 ,所以
,所以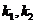 是方程
是方程
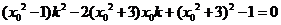 的两个不相等的根,从而
的两个不相等的根,从而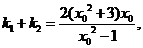
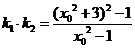 因为
因为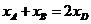 所以
所以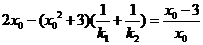 即
即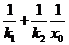
从而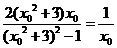 进而得
进而得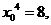
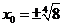 ,棕上所述,存在点
,棕上所述,存在点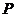 满足题意,
满足题意,
点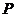 的坐标为
的坐标为