二、填空题
(一)必考题
11、从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图所示。
(I)直方图中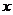 的值为;
的值为;
(II)在这些用户中,用电量落在区间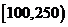 内的户数为
内的户数为
。
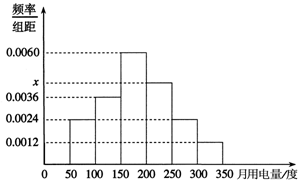
第11题图
【解析与答案】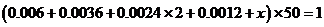 ,
,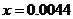
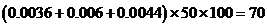
【相关知识点】频率分布直方图
12、阅读如图所示的程序框图,运行相应的程序,输出的结果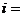 。
。
【解析与答案】5程序框图运行过程如表所示:
i | 1 | 2 | 3 | 4 | 5 |
a | 10 | 5 | 16 | 8 | 4 |
【相关知识点】程序框图
13、设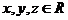 ,且满足:
,且满足: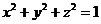 ,
,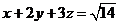 ,则
,则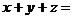 。
。
【解析与答案】由柯西不等式知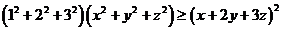 ,结合已知条件得
,结合已知条件得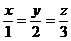 ,从而解得
,从而解得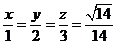 ,
,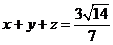 。
。
【相关知识点】柯西不等式及其等号成立的条件)
14、古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10,…,第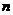 个三角形数为
个三角形数为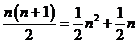 。记第
。记第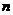 个
个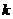 边形数为
边形数为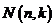
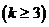 ,以下列出了部分
,以下列出了部分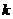 边形数中第
边形数中第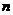 个数的表达式:
个数的表达式:
三角形数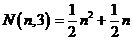
正方形数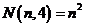
五边形数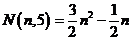
六边形数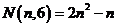
……
可以推测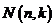 的表达式,由此计算
的表达式,由此计算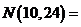 。
。
【解析与答案】观察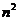 和
和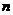 前面的系数,可知一个成递增的等差数列另一个成递减的等差数列,故
前面的系数,可知一个成递增的等差数列另一个成递减的等差数列,故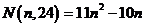 ,
,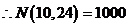
【相关知识点】归纳推理,等差数列
(二)选考题
15、如图,圆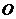 上一点
上一点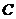 在直线
在直线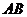 上的射影为
上的射影为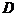 ,点
,点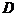 在半径
在半径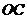 上的射影为
上的射影为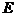 。若
。若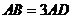 ,则
,则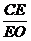 的值为。
的值为。
【解析与答案】由射影定理知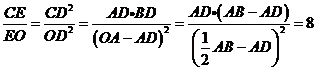
【相关知识点】射影定理,圆幂定理
16、在直角坐标系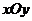 中,椭圆
中,椭圆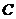 的参数方程为
的参数方程为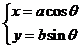
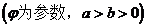 。在极坐标系(与直角坐标系
。在极坐标系(与直角坐标系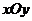 取相同的长度单位,且以原点
取相同的长度单位,且以原点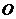 为极点,以
为极点,以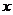 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线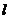 与圆
与圆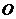 的极坐标方程分别为
的极坐标方程分别为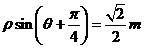
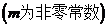 与
与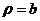 。若直线
。若直线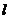 经过椭圆
经过椭圆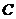 的焦点,且与圆
的焦点,且与圆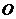 相切,则椭圆
相切,则椭圆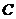 的离心率为。
的离心率为。
【解析与答案】直线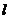 的方程是
的方程是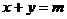 ,作出图形借助直线的斜率可得
,作出图形借助直线的斜率可得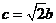 ,所以
,所以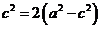 ,
,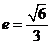
【相关知识点】极坐标与直角坐标的转化,椭圆的几何性质,直线与圆
三、解答题
17、在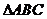 中,角
中,角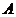 ,
,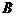 ,
,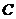 对应的边分别是
对应的边分别是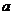 ,
,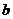 ,
,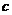 。已知
。已知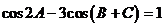 。
。
(I)求角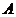 的大小;
的大小;
(II)若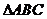 的面积
的面积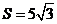 ,
,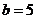 ,求
,求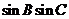 的值。
的值。
【解析与答案】(I)由已知条件得: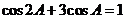
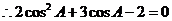 ,解得
,解得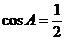 ,角
,角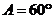
(II)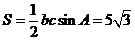
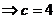 ,由余弦定理得:
,由余弦定理得: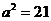 ,
,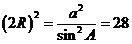
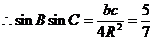
【相关知识点】二倍角公式,解三角函数方程,三角形面积,正余弦定理
18、已知等比数列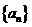 满足:
满足: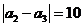 ,
,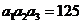 。
。
(I)求数列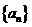 的通项公式;
的通项公式;
(II)是否存在正整数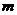 ,使得
,使得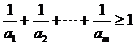 ?若存在,求
?若存在,求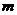 的最小值;若不存在,说明理由。
的最小值;若不存在,说明理由。
【解析与答案】(I)由已知条件得: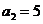 ,又
,又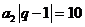 ,
,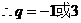 ,
,
所以数列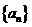 的通项或
的通项或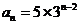
(II)若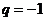 ,
,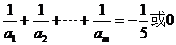 ,不存在这样的正整数
,不存在这样的正整数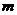 ;
;
若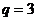 ,
,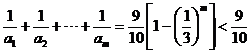 ,不存在这样的正整数
,不存在这样的正整数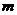 。
。
【相关知识点】等比数列性质及其求和
19、如图,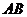 是圆
是圆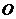 的直径,点
的直径,点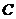 是圆
是圆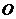 上异于
上异于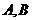 的点,直线
的点,直线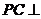 平面
平面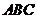 ,
,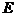 ,
,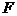 分别是
分别是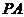 ,
,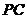 的中点。
的中点。
(I)记平面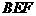 与平面
与平面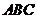 的交线为
的交线为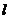 ,试判断直线
,试判断直线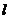 与平面
与平面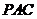 的位置关系,并加以证明;
的位置关系,并加以证明;
(II)设(I)中的直线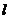 与圆
与圆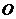 的另一个交点为
的另一个交点为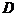 ,且点
,且点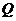 满足
满足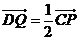 。记直线
。记直线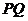 与平面
与平面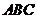 所成的角为
所成的角为 ,异面直线
,异面直线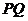 与
与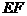 所成的角为
所成的角为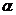 ,二面角
,二面角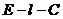 的大小为
的大小为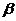 ,求证:
,求证: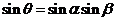 。
。
【解析与答案】(I)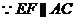 ,
,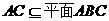 ,
,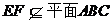
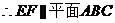
又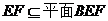
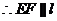

(II)连接DF,用几何方法很快就可以得到求证。(这一题用几何方法较快,向量的方法很麻烦,特别是用向量不能方便的表示角的正弦。个人认为此题与新课程中对立体几何的处理方向有很大的偏差。)
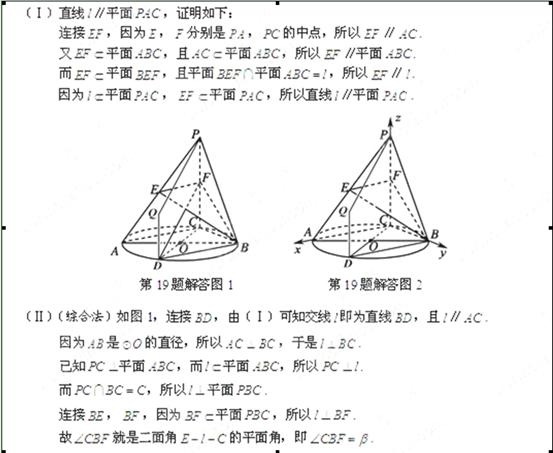


【相关知识点】












