1.D【解析】求解一元二次方程,得
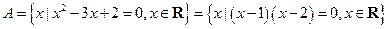
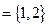 ,易知
,易知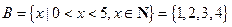 .因为
.因为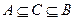 ,所以根据子集的定义,集合
,所以根据子集的定义,集合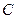 必须含有元素1,2,且可能含有元素3,4,原题即求集合
必须含有元素1,2,且可能含有元素3,4,原题即求集合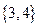 的子集个数,即有
的子集个数,即有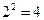 个.故选D.
个.故选D.
【点评】本题考查子集的概念,不等式,解一元二次方程.本题在求集合个数时,也可采用列举法.列出集合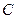 的所有可能情况,再数个数即可.来年要注意集合的交集运算,考查频度极高.
的所有可能情况,再数个数即可.来年要注意集合的交集运算,考查频度极高.
2.B【解析】由频率分布表可知:样本数据落在区间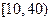 内的頻数为2+3+4=9,样本总数为
内的頻数为2+3+4=9,样本总数为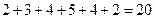 ,故样本数据落在区间
,故样本数据落在区间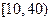 内频率为
内频率为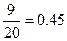 .故选B.
.故选B.
【点评】本题考查频率分布表的应用,频率的计算.对于頻数、频率等统计问题只需要弄清楚样本总数与各区间上样本的个数即可,用区间上样本的个数除以样本总数就可得到相应区间上的样本频率.来年需注意频率分布直方图与频率分布表的结合考查.
3.D【解析】由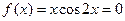 ,得
,得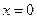 或
或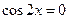 ;其中,由
;其中,由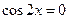 ,得
,得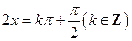 ,故
,故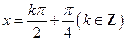 .又因为
.又因为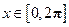 ,所以
,所以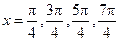 .所以零点的个数为
.所以零点的个数为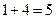 个.故选D.
个.故选D.
【点评】本题考查函数的零点,分类讨论的数学思想.判断函数的零点一般有直接法与图象法两种方法.对于三角函数的零点问题,一般需要规定自变量的取值范围;否则,如果定义域是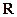 ,则零点将会有无数个;来年需注意数形结合法求解函数的零点个数,所在的区间等问题.
,则零点将会有无数个;来年需注意数形结合法求解函数的零点个数,所在的区间等问题.
4.B【解析】根据特称命题的否定,需先将存在量词改为全称量词,然后否定结论,故该命题的否定为“任意一个无理数,它的平方不是有理数”.故选B.
【点评】本题考查特称命题的否定.求解特称命题或全称命题的否定,千万别忽视了改变量词;另外,要注意一些量词的否定的书写方法,如:“都是”的否定为“不都是”,别弄成“都不是.
5.A【解析】要使直线将圆形区域分成两部分的面积之差最大,必须使过点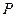 的圆的弦长达到最小,所以需该直线与直线
的圆的弦长达到最小,所以需该直线与直线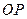 垂直即可.又已知点
垂直即可.又已知点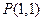 ,则
,则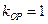 ,故所求直线的斜率为-1.又所求直线过点
,故所求直线的斜率为-1.又所求直线过点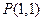 ,故由点斜式得,所求直线的方程为
,故由点斜式得,所求直线的方程为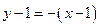 ,即
,即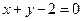 .故选A.
.故选A.
【点评】本题考查直线、线性规划与圆的综合运用,数形结合思想.本题的解题关键是通过观察图形发现当面积之差最大时,所求直线应与直线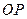 垂直,利用这一条件求出斜率,进而求得该直线的方程.来年需注意直线与圆相切的相关问题.
垂直,利用这一条件求出斜率,进而求得该直线的方程.来年需注意直线与圆相切的相关问题.
6.B【解析】特殊值法:当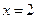 时,
时,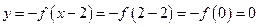 ,故可排除D项;当
,故可排除D项;当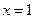 时,
时,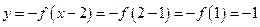 ,故可排除A,C项;所以由排除法知选B.
,故可排除A,C项;所以由排除法知选B.
【点评】本题考查函数的图象的识别.有些函数图象题,从完整的性质并不好去判断,作为徐总你则提,可以利用特殊值法(特殊点),特性法(奇偶性,单调性,最值)结合排除法求解,既可以节约考试时间,又事半功倍.来年需注意含有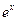 的指数型函数或含有
的指数型函数或含有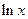 的对数型函数的图象的识别.
的对数型函数的图象的识别.
7.C 同理7
【解析】设数列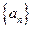 的公比为
的公比为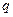 .对于①,
.对于①,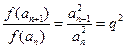 ,是常数,故①符合条件;对于②,
,是常数,故①符合条件;对于②,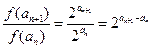 ,不是常数,故②不符合条件;对于③,
,不是常数,故②不符合条件;对于③,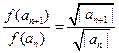
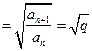 ,是常数,故③符合条件;对于④,
,是常数,故③符合条件;对于④, 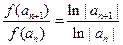 ,不是常数,故④不符合条件.由“保等比数列函数”的定义知应选C.
,不是常数,故④不符合条件.由“保等比数列函数”的定义知应选C.
【点评】本题考查等比数列的新应用,函数的概念.对于创新性问题,首先要读懂题意,然后再去利用定义求解,抓住实质是关键.来年需要注意数列的通项,等比中项的性质等.
8.D【解析】因为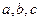 为连续的三个正整数,且
为连续的三个正整数,且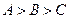 ,可得
,可得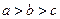 ,所以
,所以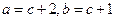 ①;又因为已知
①;又因为已知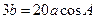 ,所以
,所以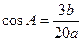 ②.由余弦定理可得
②.由余弦定理可得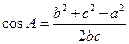 ③,则由②③可得
③,则由②③可得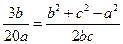 ④,联立①④,得
④,联立①④,得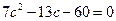 ,解得
,解得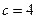 或
或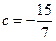 (舍去),则
(舍去),则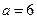 ,
,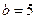 .故由正弦定理可得,
.故由正弦定理可得,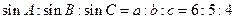 .故应选D.
.故应选D.
【点评】本题考查正、余弦定理以及三角形中大角对大边的应用.本题最终需求解三个角的正弦的比值,明显是要利用正弦定理转化为边长的比值,因此必须求出三边长.来年需注意正余弦定理与和差角公式的结合应用.
9.A【解析】当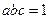 时,
时,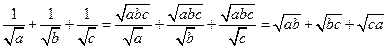 ,
,
而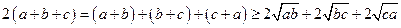 (当且仅当
(当且仅当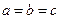 ,且
,且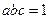 ,即
,即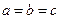 时等号成立),故
时等号成立),故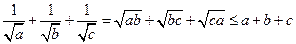 ;但当取
;但当取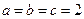 ,显然有
,显然有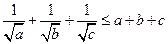 ,但
,但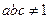 ,即由
,即由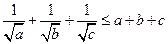 不可以推得
不可以推得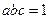 ;综上,
;综上,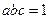 是
是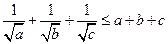 的充分不必要条件.应选A.
的充分不必要条件.应选A.
【点评】本题考查充要条件的判断,不等式的证明.判断充要条件,其常规方法是首先需判断条件能否推得结论,然后需判断结论能否推得条件;来年需注意充要条件与其他知识(如向量,函数)等的结合考查.
10.C 同理8
【解析】如图,不妨设扇形的半径为2a,如图,记两块白色区域的面积分别为S1,S2,两块阴影部分的面积分别为S3,S4,
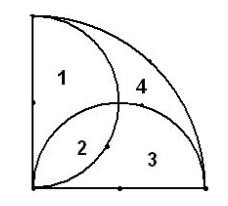
则S1+S2+S3+S4=S扇形OAB=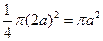 ①,
①,
而S1+S3 与S2+S3的和恰好为一个半径为a的圆,即S1+S3 +S2+S3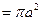 ②.
②.
①-②得S3=S4,由图可知S3=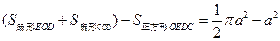 ,所以.
,所以. 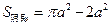 .
.
由几何概型概率公式可得,此点取自阴影部分的概率
P=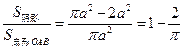 .
.
【点评】本题考查古典概型的应用以及观察推理的能力.本题难在如何求解阴影部分的面积,即如何巧妙地将不规则图形的面积化为规则图形的面积来求解.来年需注意几何概型在实际生活中的应用.
11. 6【解析】设抽取的女运动员的人数为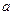 ,则根据分层抽样的特性,有
,则根据分层抽样的特性,有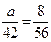 ,解得
,解得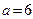 .故抽取的女运动员为6人.
.故抽取的女运动员为6人.
【点评】本题考查分层抽样的应用.本题实际是承接2012奥运会为题材,充分展示数学知识在生活中的应用.分层抽样时,各样本抽取的比例应该是一样的,即为抽样比. 来年需注意系统抽样的考查或分层抽样在解答题中作为渗透考查.
12. 3【解析】因为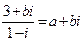 ,所以
,所以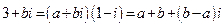 .又因为
.又因为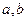 都为实数,故由复数的相等的充要条件得
都为实数,故由复数的相等的充要条件得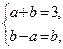 解得
解得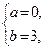 所以
所以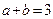 .
.
【点评】本题考查复数的相等即相关运算.本题若首先对左边的分母进行复数有理化,也可以求解,但较繁琐一些.来年需注意复数的几何意义,基本概念(共轭复数),基本运算等的考查.
13.(Ⅰ)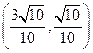 ;(Ⅱ)
;(Ⅱ)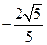
【解析】(Ⅰ)由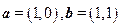 ,得
,得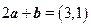 .设与
.设与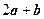 同向的单位向量为
同向的单位向量为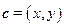 ,则
,则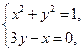 且
且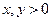 ,解得
,解得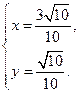 故
故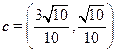 .即与
.即与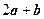 同向的单位向量的坐标为
同向的单位向量的坐标为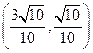 .
.
(Ⅱ)由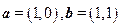 ,得
,得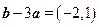 .设向量
.设向量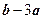 与向量
与向量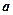 的夹角为
的夹角为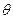 ,则
,则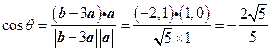 .
.
【点评】本题考查单位向量的概念,平面向量的坐标运算,向量的数量积等.与某向量同向的单位向量一般只有1个,但与某向量共线的单位向量一般有2个,它包含同向与反向两种.不要把两个概念弄混淆了. 来年需注意平面向量基本定理,基本概念以及创新性问题的考查.












