一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.方程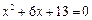 的一个根是
的一个根是
A.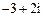 B.
B.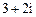 C.
C.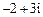 D.
D.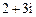
考点分析:本题考察复数的一元二次方程求根.
难易度:★
解析:根据复数求根公式: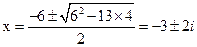 ,所以方程的一个根为
,所以方程的一个根为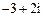
答案为A.
2.命题“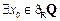 ,
,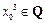 ”的否定是
”的否定是
A.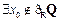 ,
,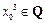 B.
B.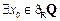 ,
,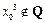
C.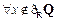 ,
,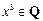 D.
D.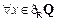 ,
,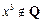
考点分析:本题主要考察常用逻辑用语,考察对命题的否定和否命题的区别.
难易度:★

解析:根据对命题的否定知,是把谓词取否定,然后把结论否定。因此选D
3.已知二次函数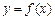 的图象如图所示,则它与
的图象如图所示,则它与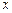 轴所围图形的面积为
轴所围图形的面积为

A.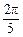 B.
B.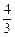
C.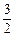 D.
D.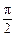
考点分析:本题考察利用定积分求面积.
难易度:★
解析:根据图像可得: 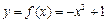 ,再由定积分的几何意义,可求得面积为
,再由定积分的几何意义,可求得面积为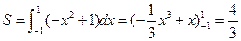 .
.
4.已知某几何体的三视图如图所示,则该几何体的体积为
A.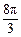 B.
B.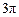
C.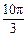 D.
D.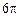
考点分析:本题考察空间几何体的三视图.
难易度:★
解析:显然有三视图我们易知原几何体为 一个圆柱体的一部分,并且有正视图知是一个1/2的圆柱体,底面圆的半径为1,圆柱体的高为6,则知所求几何体体积为原体积的一半为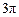 .选B.
.选B.
5.设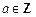 ,且
,且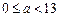 ,若
,若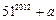 能被13整除,则
能被13整除,则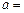
A.0 B.1
C.11 D.12
考点分析:本题考察二项展开式的系数.
难易度:★
解析:由于
51=52-1,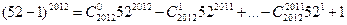 ,
,
又由于13|52,所以只需13|1+a,0≤a<13,所以a=12选D.
6.设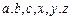 是正数,且
是正数,且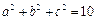 ,
,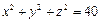 ,
,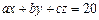 ,
,
则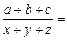
A.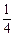 B.
B.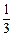
C.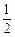 D.
D.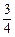
考点分析:本题主要考察了柯西不等式的使用以及其取等条件.
难易度:★★
解析:由于
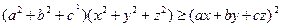
等号成立当且仅当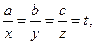 则a=t x b=t y c=t z ,
则a=t x b=t y c=t z ,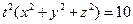
所以由题知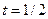
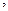 又
又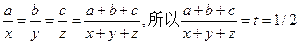 ,答案选C.
,答案选C.
7.定义在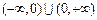 上的函数
上的函数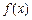 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列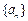 ,
, 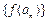 仍
仍
是等比数列,则称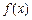 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在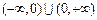 上的如下函
上的如下函
数:
①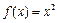 ; ②
; ②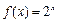 ; ③
; ③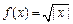 ; ④
; ④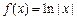 .
.
则其中是“保等比数列函数”的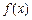 的序号为
的序号为
A.① ② B.③ ④ C.① ③ D.② ④
考点分析:本题考察等比数列性质及函数计算.
难易度:★
解析:等比数列性质,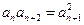 ,①
,①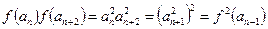 ; ②
; ②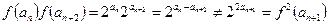 ;③
;③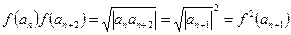 ;④
;④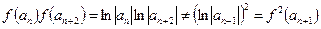 .选C
.选C
8.如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆. 在扇形OAB内随机取一点,则此点取自阴影部分的概率是

A.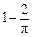 B.
B.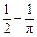
C.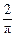 D.
D.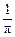
考点分析:本题考察几何概型及平面图形面积求法.
难易度:★
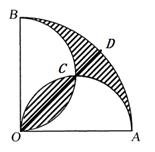
解析:令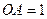 ,扇形OAB为对称图形,ACBD围成面积为
,扇形OAB为对称图形,ACBD围成面积为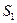 ,围成OC为
,围成OC为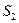 ,作对称轴OD,则过C点。
,作对称轴OD,则过C点。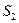 即为以OA为直径的半圆面积减去三角形OAC的面积,
即为以OA为直径的半圆面积减去三角形OAC的面积,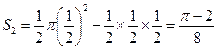 。在扇形OAD中
。在扇形OAD中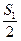 为扇形面积减去三角形OAC面积和
为扇形面积减去三角形OAC面积和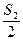 ,
,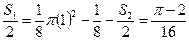 ,
,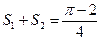 ,扇形OAB面积
,扇形OAB面积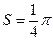 ,选A.
,选A.
9.函数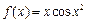 在区间
在区间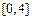 上的零点个数为
上的零点个数为
A.4 B.5
C.6 D.7
考点分析:本题考察三角函数的周期性以及零点的概念.
难易度:★
解析: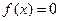 ,则
,则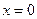 或
或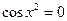 ,
,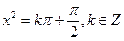 ,又
,又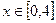 ,
,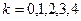
所以共有6个解.选C.
10.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径. “开立圆术”相当于给出了已知球的体积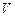 ,求其直径
,求其直径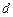 的一个近似公式
的一个近似公式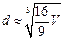 . 人们还用过一些类似的近似公式. 根据
. 人们还用过一些类似的近似公式. 根据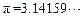 判断,下列近似公式中最精确的一个是
判断,下列近似公式中最精确的一个是
A.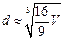 B.
B.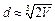 C.
C.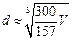 D.
D.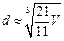
考点分析:考察球的体积公式以及估算.
难易度:★★
解析:
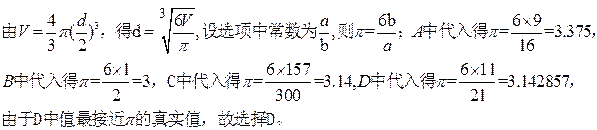
二、填空题:本大题共6小题,考生共需作答5小题,每小题5分,共25分. 请将答案填在答题卡对应题号的位置上. 答错位置,书写不清,模棱两可均不得分.
(一)必考题(11—14题)
11.设△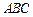 的内角
的内角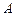 ,
,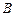 ,
,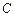 所对的边分别为
所对的边分别为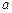 ,
,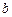 ,
,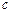 . 若
. 若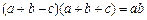 ,则角
,则角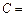 .
.
考点分析:考察余弦定理的运用.
难易度:★
解析:
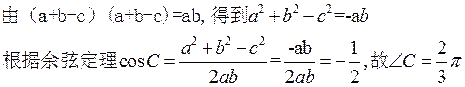
12.阅读如图所示的程序框图,运行相应的程序,输出的结果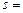 .
.
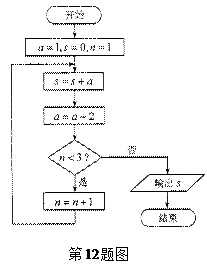
考点分析:本题考查程序框图.
难易度:★★
解析:程序在运行过程中各变量的值如下表示:
第一圈循环:当n=1时,得s=1,a=3.
第二圈循环: 当n=2时,得s=4,a=5
第三圈循环:当n=3时,得s=9,a=7
此时n=3,不再循环,所以解s=9 .
13.回文数是指从左到右读与从右到左读都一样的正整数.如22,121,3443,94249等.显然2位回文数有9个:11,22,33,…,99.3位回文数有90个:101,111,121,…,191,202,…,999.则
(Ⅰ)4位回文数有 个;
(Ⅱ)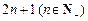 位回文数有 个.
位回文数有 个.
考点分析:本题考查排列、组合的应用.
难易度:★★
解析:(Ⅰ)4位回文数只用排列前面两位数字,后面数字就可以确定,但是第一位不能为0,有9(1~9)种情况,第二位有10(0~9)种情况,所以4位回文数有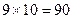 种。
种。
答案:90
(Ⅱ)法一、由上面多组数据研究发现,2n+1位回文数和2n+2位回文数的个数相同,所以可以算出2n+2位回文数的个数。2n+2位回文数只用看前n+1位的排列情况,第一位不能为0有9种情况,后面n项每项有10种情况,所以个数为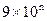 .
.
法二、可以看出2位数有9个回文数,3位数90个回文数。计算四位数的回文数是可以看出在2位数的中间添加成对的“00,11,22,……99”,因此四位数的回文数有90个按此规律推导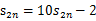 ,而当奇数位时,可以看成在偶数位的最中间添加0~9这十个数,因此
,而当奇数位时,可以看成在偶数位的最中间添加0~9这十个数,因此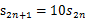 ,则答案为
,则答案为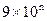 .
.
14.如图,双曲线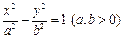 的两顶点为
的两顶点为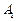 ,
,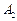 ,虚轴两端点为
,虚轴两端点为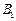 ,
,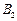 ,两焦点为
,两焦点为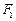 ,
,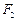 . 若以
. 若以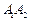 为直径的圆内切于菱形
为直径的圆内切于菱形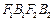 ,切点分别为
,切点分别为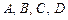 . 则
. 则

(Ⅰ)双曲线的离心率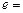 ;
;
(Ⅱ)菱形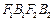 的面积
的面积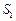 与矩形
与矩形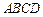 的面积
的面积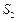 的比值
的比值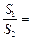 .
.
考点分析:本题考察双曲线中离心率及实轴虚轴的相关定义,以及一般平面几何图形的面积计算.
难易度:★★
解析:(Ⅰ)由于以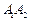 为直径的圆内切于菱形
为直径的圆内切于菱形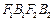 ,因此点
,因此点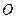 到直线
到直线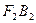 的距离为
的距离为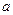 ,又由于虚轴两端点为
,又由于虚轴两端点为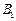 ,
,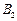 ,因此
,因此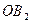 的长为
的长为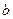 ,那么在
,那么在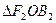 中,由三角形的面积公式知,
中,由三角形的面积公式知,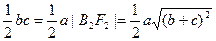 ,又由双曲线中存在关系
,又由双曲线中存在关系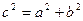 联立可得出
联立可得出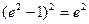 ,根据
,根据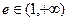 解出
解出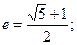
(Ⅱ)设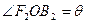 ,很显然知道
,很显然知道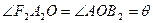 ,
,![]() 因此
因此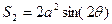 .在
.在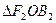 中求得
中求得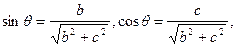 故
故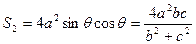 ;
;
菱形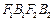 的面积
的面积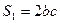 ,再根据第一问中求得的
,再根据第一问中求得的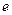 值可以解出
值可以解出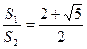 .
.
(二)选考题(请考生在第15、16两题中任选一题作答,请先在答题卡指定位置将你所选的题目序号后的方框用2B铅笔涂黑. 如果全选,则按第15题作答结果计分.)
15.(选修4-1:几何证明选讲)
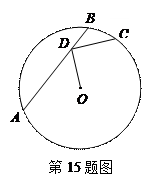
如图,点D在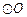 的弦AB上移动,
的弦AB上移动,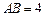 ,连接OD,过点D作
,连接OD,过点D作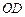 的垂线交
的垂线交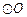 于点C,则CD的最大值为 .
于点C,则CD的最大值为 .
考点分析:本题考察直线与圆的位置关系
难易度:★
解析:(由于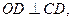 因此
因此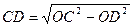 ,线段
,线段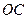 长为定值,
长为定值,
即需求解线段 长度的最小值,根据弦中点到圆心的距离最短,此
长度的最小值,根据弦中点到圆心的距离最短,此
时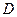 为
为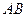 的中点,点
的中点,点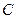 与点
与点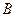 重合,因此
重合,因此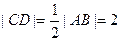 .
.
16.(选修4-4:坐标系与参数方程)
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴
建立极坐标系. 已知射线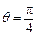 与曲线
与曲线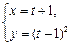 (t为参数)
(t为参数)
相交于A,B两点,则线段AB的中点的直角坐标为 .
考点分析:本题考察平面直角坐标与极坐标系下的曲线方程交点.
难易度:★
解析: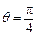 在直角坐标系下的一般方程为
在直角坐标系下的一般方程为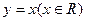 ,将参数方程
,将参数方程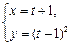 (t为参数)转化为直角坐标系下的一般方程为
(t为参数)转化为直角坐标系下的一般方程为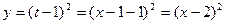 表示一条抛物线,联立上面两个方程消去
表示一条抛物线,联立上面两个方程消去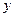 有
有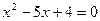 ,设
,设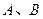 两点及其中点
两点及其中点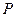 的横坐标分别为
的横坐标分别为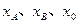 ,则有韦达定理
,则有韦达定理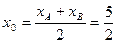 ,又由于点
,又由于点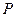 点在直线
点在直线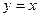 上,因此
上,因此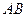 的中点
的中点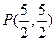 .
.












