第Ⅱ卷(共90分)
二、填空题:本大题共4小题,每小题4分,共16分.
(13)如图,正方体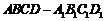 的棱长为1,E为线段
的棱长为1,E为线段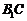 上的一点,则三棱锥
上的一点,则三棱锥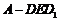 的体积为_____.
的体积为_____.
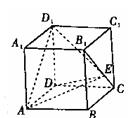
【解析】以△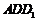 为底面,则易知三棱锥的高为1,故
为底面,则易知三棱锥的高为1,故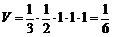 .
.
【答案】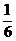
(14)右图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为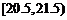 ,
,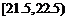 ,
,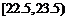 ,
,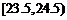 ,
,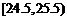 ,
,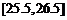 .已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为____.
.已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为____.
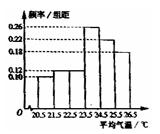
【解析】最左边两个矩形面积之和为0.10×1+0.12×1=0.22,总城市数为11÷0.22=50,最右面矩形面积为0.18×1=0.18,50×0.18=9.
【答案】9
(15)若函数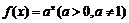 在[-1,2]上的最大值为4,最小值为m,且函数
在[-1,2]上的最大值为4,最小值为m,且函数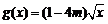 在
在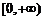 上是增函数,则a=____.
上是增函数,则a=____.
【解析】当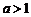 时,有
时,有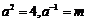 ,此时
,此时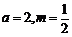 ,此时
,此时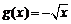 为减函数,不合题意.若
为减函数,不合题意.若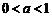 ,则
,则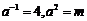 ,故
,故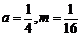 ,检验知符合题意.
,检验知符合题意.
【答案】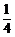
(16)如图,在平面直角坐标系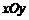 中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,
中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,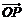 的坐标为____.
的坐标为____. 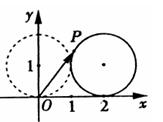
【解析】因为圆心移动的距离为2,所以劣弧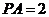 ,即圆心角
,即圆心角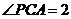 ,
,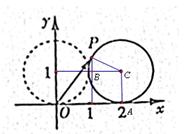 ,则
,则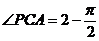 ,所以
,所以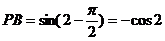 ,
,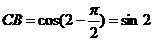 ,所以
,所以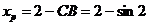 ,
,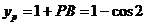 ,所以
,所以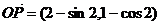 .
.
另解:根据题意可知滚动制圆心为(2,1)时的圆的参数方程为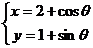 ,且
,且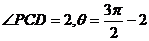 ,则点P的坐标为
,则点P的坐标为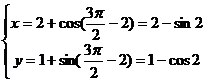 ,即
,即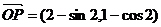 .
.
【答案】