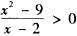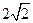第Ⅱ卷
二。填空题:本大题共5小题,每小题5分,共25分。
【答案】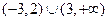
【解析】不等式可化为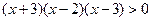 采用穿针引线法解不等式即可.
采用穿针引线法解不等式即可.
12.设单位向量m=(x,y),b=(2,-1)。若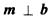 ,则
,则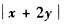 =_______________
=_______________
【答案】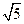
【解析】由已知可得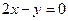 ,又因为m为单位向量所以
,又因为m为单位向量所以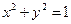 ,联立解得
,联立解得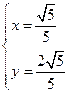 或
或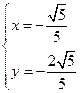 代入所求即可.
代入所求即可.
13.等比数列{an}的前n项和为Sn,公比不为1。若a1=1,且对任意的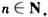 都有an+2+an+1-2an=0,则S5=_________________。
都有an+2+an+1-2an=0,则S5=_________________。
【答案】11
【解析】由已知可得公比q=-2,则a1=1可得S5。
14.过直线x+y-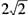 =0上点P作圆x2+y2=1的两条切线,若两条切
=0上点P作圆x2+y2=1的两条切线,若两条切 线的夹角是60°,则点P的坐标是__________。
线的夹角是60°,则点P的坐标是__________。
【答案】(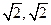 )
)
【解析】本题主要考查数形结合的思想,设p(x,y),则由已知可得po(0为原点)与切线的夹角为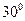 ,则|po|=2,由
,则|po|=2,由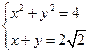 可得
可得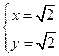 .
.
15.下图是某算法的程序框图,则程序运行后输入的结果是_________。

【答案】3
【解析】当k=1,a=1,T=1
当k=2,a=0,T=1
当k=3,a=0,T=1
当k=4,a=1,T=2
当k=5,a=1,T=3,则此时k=k+1=6所以输出T=3.
三、解答题:本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分12分)
△ABC中,角A,B,C的对边分别为a,b,c。已知3cos(B-C)-1=6cosBcosC。
(1)求cosA;
【解析】(1)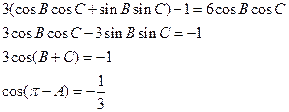 则
则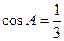 .
.
(2) 由(1)得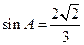 ,由面积可得bc=6①,则根据余弦定理
,由面积可得bc=6①,则根据余弦定理
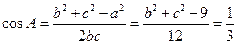 则
则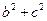 =13②,①②
=13②,①② 两式联立可得b=1,c=5或b=5,c=1.
两式联立可得b=1,c=5或b=5,c=1.