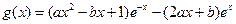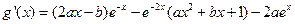17.(本小题满分12分)
已知数列|an|的前n项和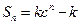 (其中c
(其中c ,k为常数),且a2=4,a6=8a3
,k为常数),且a2=4,a6=8a3
(1)求an;
(2)求数列{nan}的前n项和Tn。
【解析】(1)当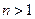 时,
时,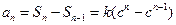
则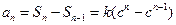
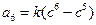 ,
,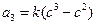
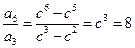 ,∴c=2.∵a2=4,即
,∴c=2.∵a2=4,即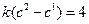 ,解得k=2,∴
,解得k=2,∴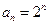 (n)1)
(n)1)
当n=1时,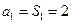
综上所述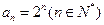
(2) 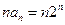 ,则
,则
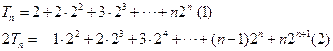 (1)-(2)得
(1)-(2)得
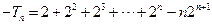
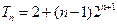
18.(本小题满分12分)
如图,从A1(1,0,0),A2(2,0,0),B1(0,1,0,)B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点。
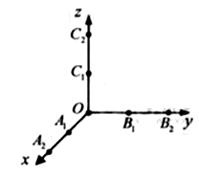
(1) 求这3点与原点O恰好是正三棱锥的四个顶点的概率;
(2) 求这3点与原点O共面的概率。
【解析】(1)总的结果数为20种,则满足条件的种数为2种所以所求概率为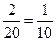
(2)满足条件的情况为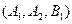 ,
,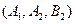 ,
,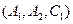 ,
,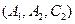 ,
,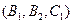 ,
,
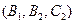 ,所以所求概率为
,所以所求概率为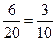 .
.
19. (本小题满分12分)
如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4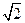 ,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.
,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.
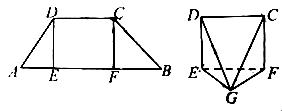
(1) 求证:平面DEG⊥平面CFG;
(2)  求多面体C
求多面体C DEFG的体积。
DEFG的体积。
【解析】(1)由已知可得AE=3,BF=4,则折叠完后EG=3,GF=4,又因为EF=5,所以可得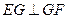
又因为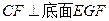 ,可得
,可得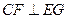 ,即
,即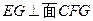 所以平面DEG⊥平面CFG.
所以平面DEG⊥平面CFG.
(2)过G作GO垂直于EF,GO 即为四棱锥G-EFCD的高,所以所求体积为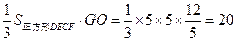
20.(本小题满分13分)
已知三点O(0,0),A(-2,1) ,B(2,1),曲线C上任意一点M(x,y)满足
,B(2,1),曲线C上任意一点M(x,y)满足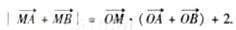
(1)求曲线C的方程;
(2)点Q(x0,y0)(-2<x0<2)是曲线C上动点,曲线C在点Q处的切线为l,点P的坐标是(0,-1),l与PA,PB分别交于点D,E,求△QAB与△PDE的面积之比。
 【解析】(1)
【解析】(1)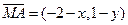 ,
,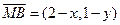 ,
,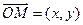 ,
,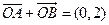
代入式子可得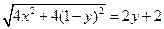 整理得
整理得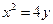
(2)
21.(本小题满分14分)
已知函数f(x)=(ax2+bx+c)ex在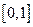 上单调递减且满足f(0)=1,f(1)=0.
上单调递减且满足f(0)=1,f(1)=0.
(1)求a的取值范围;
(2)设g(x)= f(-x)- f′(x),求g(x)在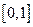 上的最大值和最小值。
上的最大值和最小值。
【解析】(1)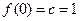 ,
,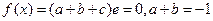 ,
,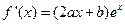 因为在[0,1]上单调递减则令
因为在[0,1]上单调递减则令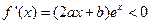 即
即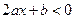 解得
解得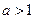
(2)