一.选择题:本小题共12题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知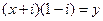 ,则实数
,则实数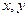 分别为
分别为
A.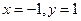 B.
B.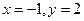
C.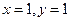 D.
D.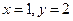
【答案】D
【命题意图】本题主要考查复数的乘法运算及实数的条件.
【解析】∵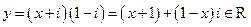 ,∴
,∴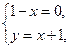 即
即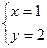 .
.
2.若集合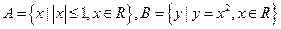 ,则
,则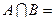
A.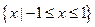 B.
B.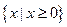
C.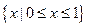 D.
D.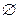
【答案】C
【命题意图】本题主要考查函数的定义域与值域及集合的交集运算.
【解析】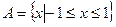 ,
,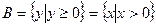 ,∴
,∴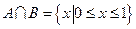 .故选C.
.故选C.
3.不等式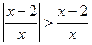 的解集是
的解集是
A.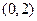 B.
B.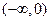
C.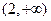 D.
D.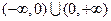
【答案】A
【命题意图】本题主要考查绝对值不等式与分式不等式的解法.
【解析】由已知,原不等式等价于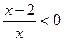 ,即
,即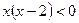 .∴解集为
.∴解集为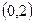 .
.
4.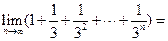
A.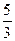 B.
B.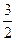 C.
C.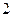 D.不存在
D.不存在
【答案】B
【命题意图】本题主要考查等比数列的求和公式与简单的极限.
【解析】原式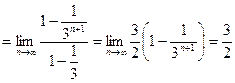 .
.
5.等比数列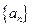 中,
中,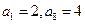 ,函数
,函数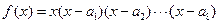 ,则
,则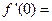
A.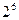 B.
B.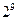 C.
C.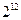 D.
D.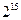

6.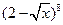 展开式中不含
展开式中不含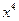 项的系数的和为
项的系数的和为
A.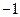 B.
B.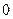 C.
C.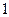 D.
D.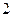
【答案】B
【命题意图】本题主要考查二项式定理通项的运用.
【解析】令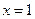 ,则
,则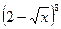 中所有项的系数和为1.
中所有项的系数和为1.
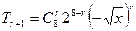
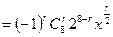 ,则
,则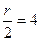 ,即
,即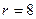 .∴含
.∴含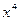 项的系数为
项的系数为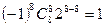 ,∴不含
,∴不含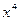 项的系数为
项的系数为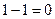 .
.
7.E,F是等腰直角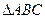 斜边AB上的三等分点,则
斜边AB上的三等分点,则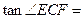
A.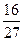 B.
B.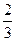 C.
C.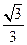 D.
D.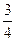
【答案】D
【命题意图】本题主要考查向量 夹角公式及坐标法的应用.
夹角公式及坐标法的应用.
【解析】以C为坐标原点,分别以CA,CB所在直线为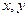 轴建立平面直角坐标系.不妨设CA=CB=3
轴建立平面直角坐标系.不妨设CA=CB=3 ,则A
,则A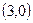 ,B
,B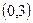 .∵E,F是斜边AB的三等分点,∴E
.∵E,F是斜边AB的三等分点,∴E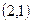 ,F
,F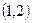 .
.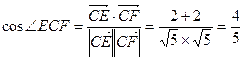 ,∵
,∵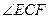 为锐角,
为锐角,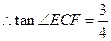 .
.
8.直线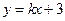 与圆
与圆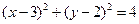 相交于M,N两点,若
相交于M,N两点,若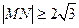 ,则
,则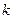 的取值范围是
的取值范围是
A.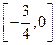 B.
B.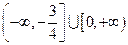
C.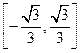 D.
D.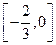

9.给出下列三个命题:
①函数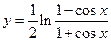 与
与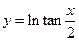 是同一函数;
是同一函数;
②若函数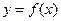 与
与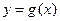 的图像关于直线
的图像关于直线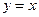 对称,则函数
对称,则函数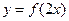 与
与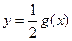 的图像也关于直线
的图像也关于直线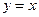 对称;
对称;
③若奇函数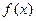 对定义域内任意
对定义域内任意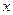 都有
都有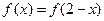 ,则
,则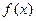 为周期函数.
为周期函数.
其中真命题是
A.①② B.①③ C.②③ D.②
【答案】C
【命题意图】本题主要考查函数、反函数的概念及奇偶性、周期性以及逻辑推理能力.
【解析】①中,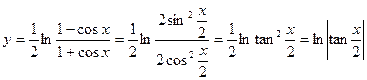 与
与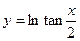

10.过正方体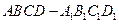 的顶点A作直线
的顶点A作直线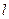 ,使
,使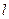 与棱
与棱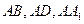 所成的角都相等,这样的直线
所成的角都相等,这样的直线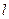 可以作
可以作
A.1条 B.2条
C.3条 D.4条
【答案】D
【命题意图】本题主要考查空间想象能力.
【解析】由正方体易得体对角线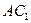 就是其中一条与
就是其中一条与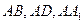 所成的角都相等的直线,而且所求角的大小为
所成的角都相等的直线,而且所求角的大小为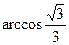 .可以想象一下,把正方体中这三边分别延长会构造出以A为顶点的另三个与已知正方体全等的正方体,各自都有一条过A点的体对角线符合条件.共4条.
.可以想象一下,把正方体中这三边分别延长会构造出以A为顶点的另三个与已知正方体全等的正方体,各自都有一条过A点的体对角线符合条件.共4条.
11.一位国王的铸币大臣在每箱100枚的硬币中各参入了一枚劣币,国王怀疑大臣作弊,他用两种方法来检测.方法一:在10箱中各任意抽查一枚;方法二:在5箱中各任意抽查两枚.国王用方法一、二能发现至少一枚劣币的概率分别记为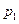 和
和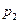 .则
.则
A.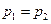 B.
B.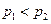 C.
C.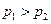 D.以上三种情况都有可能
D.以上三种情况都有可能
【答案】B
【命题意图】本题主要考查概率问题,等可能事件与对立事件及近似估算 法.
法.
【解析】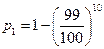 ,
,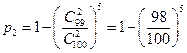 ,其中
,其中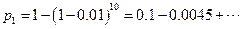 ,
,
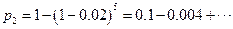 ∴
∴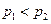 .
.
12.如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记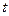 时刻五角星露出水面部分的图形面积为
时刻五角星露出水面部分的图形面积为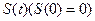 ,则导函数
,则导函数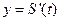 的图像大致为
的图像大致为


二.填空题:本大题共4小题,每小题4分,共16分.请把答案填写在答题卡上.
13.已知向量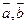 满足
满足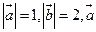 与
与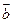 的夹角为60°,则
的夹角为60°,则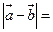 ______________.
______________.
【答案】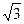
【命题意图】本题主要考查向量模的计算.
【解析】∵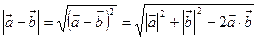
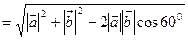 .将已知数据代入上式,∴
.将已知数据代入上式,∴ 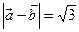 .
.
14.将6位志愿者分成4组,其中两个组各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有_________种(用数字作答).
【答案】1080
【命题意图 】本题主要考查排列组合知识中的平均分组再分配问题.
】本题主要考查排列组合知识中的平均分组再分配问题.
【解析】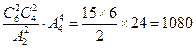 .
.
15.点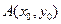 在双曲线
在双曲线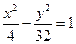 的右支上,若点A到右焦点的距离等于
的右支上,若点A到右焦点的距离等于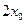 ,则
,则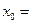 __________.
__________.
【答案】2
【命题意图】本题主要考查圆锥曲线的第二定义.
【解析】双曲线的离心率e=3.右准线为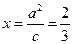 .所以得到A到准线的距离d为
.所以得到A到准线的距离d为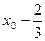 .所以
.所以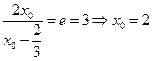 .
.
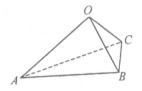
16.如图,在三棱锥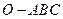 中,三条棱
中,三条棱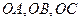 两两垂直,且
两两垂直,且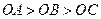 ,分别经过三条棱
,分别经过三条棱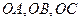 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为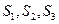 ,则
,则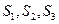 的大小关系为________________.
的大小关系为________________.