第I卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)复数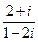 的共轭复数是
的共轭复数是
(A)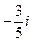 (B)
(B)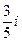 (C)
(C)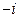 (D)
(D)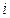
解析: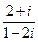 =
=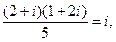 共轭复数为C
共轭复数为C
(2)下列函数中,既是偶函数又在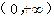 单调递增的函数是
单调递增的函数是
(A)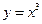 (B)
(B) 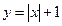 (C)
(C)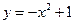 (D)
(D) 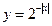
解析:由图像知选B
(3)执行右面的程序框图,如果输入的N是6,那么输出的p是
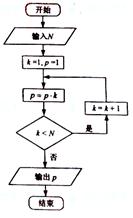
(A)120
(B)720
(C)1440
(D)5040
解析:框图表示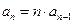 ,且
,且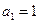 所求
所求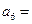 720
720
选B
(4)有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为
(A)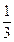 (B)
(B)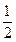 (C)
(C)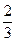 (D)
(D)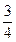
解析;每个同学参加的情形都有3种,故两个同学参加一组的情形有9种,而参加同一组的情形只有3种,所求的概率为p=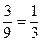 选A
选A
(5)已知角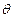 的顶点与原点重合,始边与
的顶点与原点重合,始边与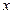 轴的正半轴重合,终边在直线
轴的正半轴重合,终边在直线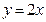 上,则
上,则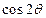 =
=
解析:由题知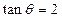 ,
,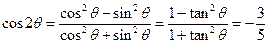 选B
选B
(A)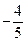 (B)
(B)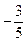 (C)
(C)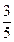 (D)
(D)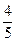
(6)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为
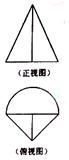
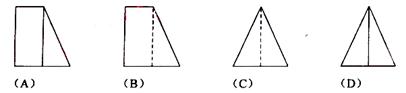
解析:条件对应的几何体是由底面棱长为r的正四棱锥沿底面对角线截出的部分与底面为半径为r的圆锥沿对称轴截出的部分构成的。故选D
(7)设直线L过双曲线C的一个焦点,且与C的一条对称轴垂直,L与C交于A ,B两点,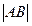 为C的实轴长的2倍,则C的离心率为
为C的实轴长的2倍,则C的离心率为
(A)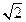 (B)
(B)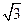 (C)2 (D)3
(C)2 (D)3
解析:通径|AB|=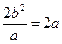 得
得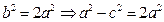 ,选B
,选B
(8)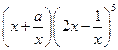 的展开式中各项系数的和为2,则该展开式中常数项为
的展开式中各项系数的和为2,则该展开式中常数项为
(A)-40 (B)-20 (C)20 (D)40
解析1.令x=1得a=1.故原式=
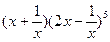 。
。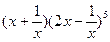
 的通项
的通项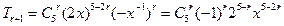 ,由5-2r=1得r=2,对应的常数项=80,由5-2r=-1得r=3,对应的常数项=-40,故所求的常数项为40 ,选D
,由5-2r=1得r=2,对应的常数项=80,由5-2r=-1得r=3,对应的常数项=-40,故所求的常数项为40 ,选D
解析2.用组合提取法,把原式看做6个因式相乘,若第1个括号提出x,从余下的5个括号中选2个提出x,选3个提出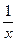 ;若第1个括号提出
;若第1个括号提出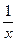 ,从余下的括号中选2个提出
,从余下的括号中选2个提出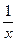 ,选3个提出x.
,选3个提出x.
故常数项=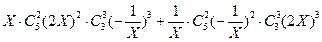 =-40+80=40
=-40+80=40
(9)由曲线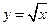 ,直线
,直线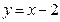 及
及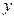 轴所围成的图形的面积为
轴所围成的图形的面积为
(A)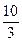 (B)4 (C)
(B)4 (C)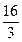 (D)6
(D)6
解析;用定积分求解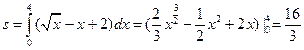 ,选C
,选C
(10)已知a与b均为单位向量,其夹角为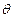 ,有下列四个命题
,有下列四个命题
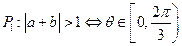
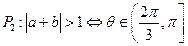
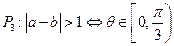
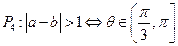
其中的真命题是
(A)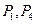 (B)
(B)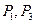 (C)
(C)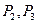 (D)
(D)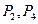
解析: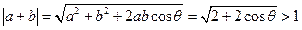 得,
得, 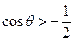 ,
,
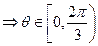 。由
。由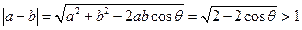 得
得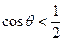
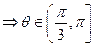 。 选A
。 选A
(11)设函数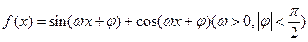 的最小正周期为
的最小正周期为 ,且
,且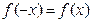 ,则
,则
(A)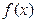 在
在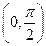 单调递减 (B)
单调递减 (B)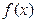 在
在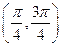 单调递减
单调递减
(C)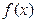 在
在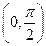 单调递增 (D)
单调递增 (D)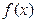 在
在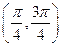 单调递增
单调递增
解析: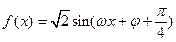 ,所以
,所以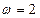 ,又f(x)为偶函数,
,又f(x)为偶函数,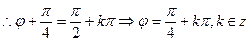 ,
,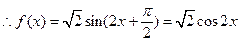 ,选A
,选A
(12)函数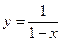 的图像与函数
的图像与函数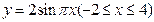 的图像所有交点的横坐标之和等于
的图像所有交点的横坐标之和等于
(A)2 (B) 4 (C) 6 (D)8
解析:图像法求解。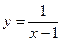 的对称中心是(1,0)也是
的对称中心是(1,0)也是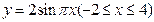 的中心,
的中心,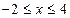 他们的图像在x=1的左侧有4个交点,则x=1右侧必有4个交点。不妨把他们的横坐标由小到大设为
他们的图像在x=1的左侧有4个交点,则x=1右侧必有4个交点。不妨把他们的横坐标由小到大设为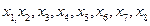 ,则
,则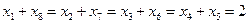 ,所以选D
,所以选D














