第Ⅱ卷

二、填空题：本大题共4小题，每小题5分。

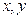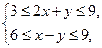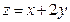（13）若变量满足约束条件则的最小值为 。

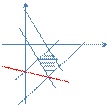
解析：画出区域图知，

当直线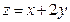过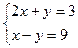的交点(4,-5)时，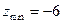

（14）在平面直角坐标系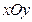中，椭圆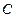的中心为原点，焦点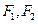在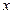轴上，离心率为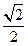。过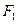的直线L交C于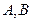两点，且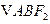的周长为16，那么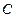的方程为 。

解析：由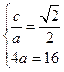得a=4.c=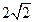,从而b=8,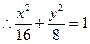为所求。

（15）已知矩形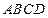的顶点都在半径为4的球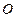的球面上，且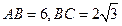,则棱锥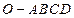的体积为 。

解析：设ABCD所在的截面圆的圆心为M,则AM=,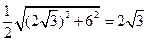

OM=，.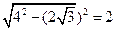

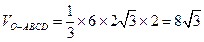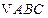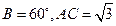（16）在中，，则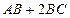的最大值为 。

解析：,,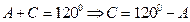

；

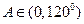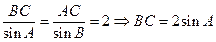
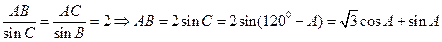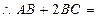
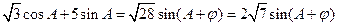，故最大值是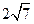

三、解答题：解答应写出文字说明，证明过程或演算步骤。

（17）（本小题满分12分）

等比数列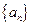的各项均为正数，且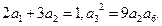

（Ⅰ)求数列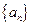的通项公式；

（Ⅱ）设 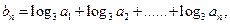求数列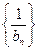的前n项和.

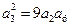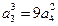解析：（Ⅰ）设数列{an}的公比为q，由得所以。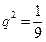

由条件可知a>0,故。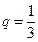

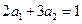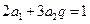由得，所以。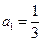

故数列{an}的通项式为an=。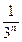

（Ⅱ ）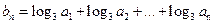

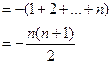
故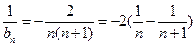

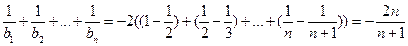
所以数列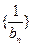的前n项和为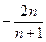

(18)(本小题满分12分)

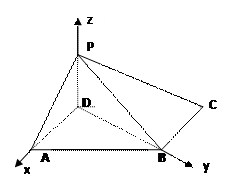
如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.

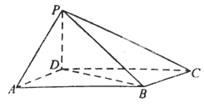
(Ⅰ)证明：PA⊥BD；

(Ⅱ)若PD=AD，求二面角A-PB-C的余弦值。

解析1：（Ⅰ）因为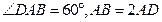, 由余弦定理得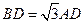

从而BD2+AD2= AB2，故BD 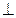AD;又PD 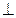底面ABCD，可得B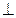D PD

所以BD 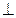平面PAD. 故 PA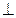BD

（Ⅱ）如图，以D为坐标原点，AD的长为单位长，射线DA为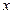轴的正半轴建立空间直角坐标系D-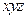，则

,,,。

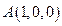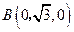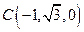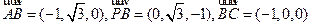
设平面PAB的法向量为n=（x,y,z），则,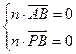

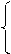即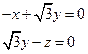

因此可取n=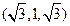

设平面PBC的法向量为m，则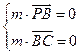

可取m=（0，-1，）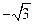

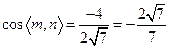
故二面角A-PB-C的余弦值为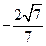

（19）（本小题满分12分）

某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品，现用两种新配方（分别称为A配方和B配方）做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：

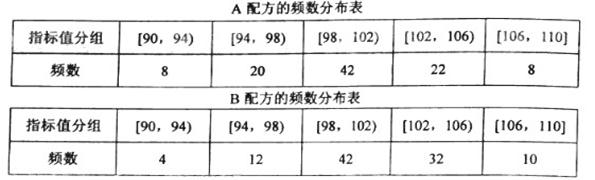
（Ⅰ）分别估计用A配方，B配方生产的产品的优质品率；

（Ⅱ）已知用B配方生成的一件产品的利润y(单位：元)与其质量指标值t的关系式为

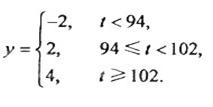
从用B配方生产的产品中任取一件，其利润记为X（单位：元），求X的分布列及数学期望.（以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）

解析：（Ⅰ）由试验结果知，用A配方生产的产品中优质的平率为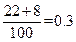，所以用A配方生产的产品的优质品率的估计值为0.3。

由试验结果知，用B配方生产的产品中优质品的频率为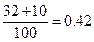，所以用B配方生产的产品的优质品率的估计值为0.42

（Ⅱ）用B配方生产的100件产品中，其质量指标值落入区间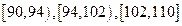的频率分别为0.04，,054,0.42，因此X的可能值为-2,2,4

P(X=-2)=0.04, P(X=2)=0.54, P(X=4)=0.42,

即X的分布列为

X的数学期望值EX=-2×0.04+2×0.54+4×0.42=2.68

点击此处下载文档(rar格式，598.37KB)