二、填空题:本大题共4小题,每小题4分,共16分.
13.执行右图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是 .
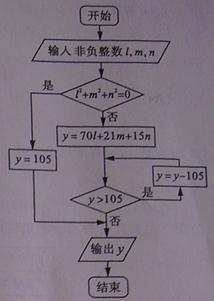
【答案】68
【解析】由输入l=2,m=3,n=5,计算得出y=278,第一次得新的y=173;第二次得新的y=68<105,输出y.
14. 若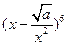 展开式的常数项为60,则常数
展开式的常数项为60,则常数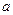 的值为 .
的值为 .
【答案】4
【解析】因为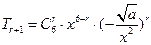 ,所以r=2, 常数项为
,所以r=2, 常数项为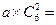 60,解得
60,解得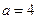 .
.
15. 设函数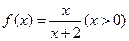 ,观察:
,观察:
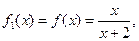
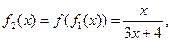
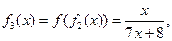
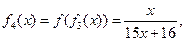
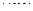
根据以上事实,由归纳推理可得:
当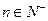 且
且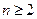 时,
时,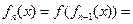 .
.
【答案】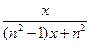
【解析】观察知:四个等式等号右边的分母为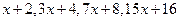 ,即
,即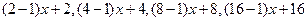 ,所以归纳出分母为
,所以归纳出分母为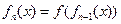 的分母为
的分母为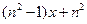 ,故当
,故当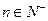 且
且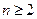 时,
时,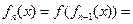
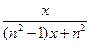 .
.
16.已知函数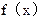 =
=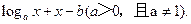 当2<a<3<b<4时,函数
当2<a<3<b<4时,函数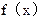
 的零点
的零点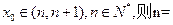 .
.
【答案】5
【解析】方程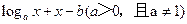 =0的根为
=0的根为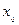 ,即函数
,即函数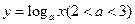 的图象与函数
的图象与函数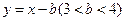 的交点横坐标为
的交点横坐标为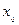 ,且
,且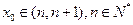 ,结合图象,因为当
,结合图象,因为当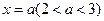 时,
时,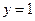 ,此时对应直线上
,此时对应直线上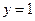 的点的横坐标
的点的横坐标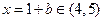 ;当
;当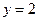 时, 对数函数
时, 对数函数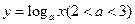 的图象上点的横坐标
的图象上点的横坐标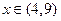 ,直线
,直线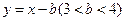 的图象上点的横坐标
的图象上点的横坐标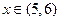 ,故所求的
,故所求的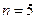 .
.
三、解答题:本大题共6小题,共74分.
17.(本小题满分12分)
在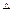 ABC中
ABC中 ,内角A,B,C的对边分别为a,b,c.已知
,内角A,B,C的对边分别为a,b,c.已知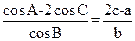 .
.
(I)求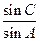 的值;
的值;
(II)若cosB=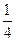 ,
,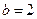 ,求
,求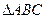 的面积.
的面积.
【解析】(Ⅰ)由正弦定理得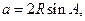
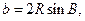
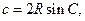 所以
所以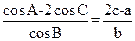 =
=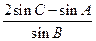 ,即
,即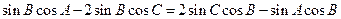 ,即有
,即有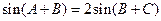 ,即
,即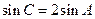 ,所以
,所以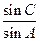 =2.
=2.
(Ⅱ)由(Ⅰ)知: 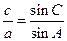 =2,即c=2a,又因为
=2,即c=2a,又因为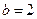 ,所以由余弦定理得:
,所以由余弦定理得:
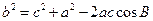 ,即
,即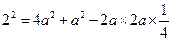 ,解得
,解得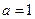 ,所以c=2,又因为cosB=
,所以c=2,又因为cosB=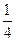 ,所以sinB=
,所以sinB=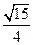 ,故
,故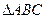 的面积为
的面积为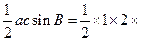
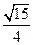 =
=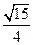 .
.
18.(本小题满分12分)
红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立。
(Ⅰ)求红队至少两名队员获胜的概率;
(Ⅱ)用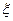 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求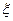 的分布列和数学期望
的分布列和数学期望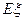 .
.
【解析】(Ⅰ)红队至少两名队员获胜的概率为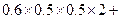
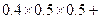
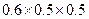 =0.55.
=0.55.
(Ⅱ)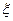 取的可能结果为0,1,2,3,则
取的可能结果为0,1,2,3,则
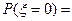
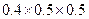 =0.1;
=0.1;
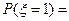
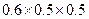 +
+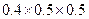 +
+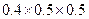 =0.35;
=0.35;
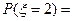
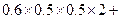
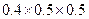 =0.4;
=0.4;
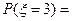
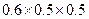 =0.15.
=0.15.
所以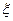 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
P | 0.1 | 0.35 | 0.4 | 0.15 |
数学期望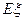 =0×0.1+1×0.35+2×0.4+3×0.
=0×0.1+1×0.35+2×0.4+3×0. 15=1.6.
15=1.6.












