19.(本小题满分12分)
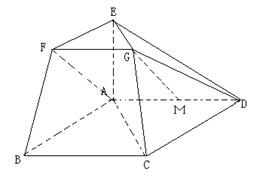
在如图所示的几何体中,四边形ABCD为平行四边形,∠ ACB=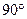 ,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC.AB=2EF.
,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC.AB=2EF.
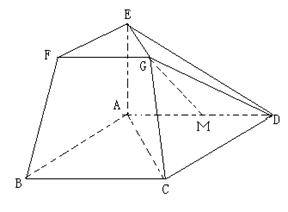
(Ⅰ)若M是线段AD的中点,求证:GM∥平面ABFE;
(Ⅱ)若AC=BC=2AE,求二面角A-BF-C的大小.
【解析】(Ⅰ)连结AF,因为EF∥AB,FG∥BC,
EF∩FG=F,所以平面EFG∥平面ABCD,又易证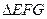 ∽
∽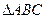 ,
,
所以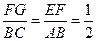 ,即
,即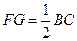 ,即
,即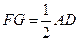 ,又M为AD
,又M为AD
的中点,所以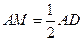 ,
, 又因为FG∥BC∥AD,所以FG∥AM,所以四边形AMGF是平行四边形,故GM∥FA,又因为GM
又因为FG∥BC∥AD,所以FG∥AM,所以四边形AMGF是平行四边形,故GM∥FA,又因为GM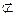 平面ABFE,FA
平面ABFE,FA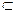 平面ABFE,所以GM∥平面ABFE.
平面ABFE,所以GM∥平面ABFE.
(Ⅱ)取AB的中点O,连结CO,因为AC=BC,所以CO⊥AB,
又因为EA⊥平面AB CD,CO
CD,CO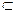 平面ABCD,所以EA⊥CO,
平面ABCD,所以EA⊥CO,
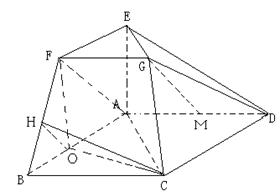
又EA∩AB=A,所以CO⊥平面ABFE,在平面ABEF内,过点O作OH⊥BF于H,连结CH,由三垂线定理知: CH⊥BF,所以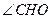 为二
为二 面角A-BF-C的平面角.
面角A-BF-C的平面角.
设AB=2EF=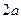 ,因为∠ ACB=
,因为∠ ACB=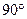 ,AC=BC=
,AC=BC=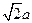 ,CO=
,CO=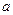 ,
,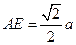 ,连结FO,容易证得FO∥EA且
,连结FO,容易证得FO∥EA且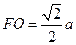 ,所以
,所以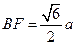 ,所以OH=
,所以OH=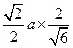 =
=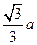 ,所以在
,所以在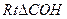 中,tan∠ CHO=
中,tan∠ CHO=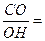
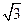 ,故∠ CHO=
,故∠ CHO=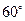 ,所以二面角A-BF-C的大小为
,所以二面角A-BF-C的大小为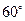 .
.
20.(本小题满分12分)
等比数列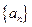 中,
中,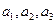 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且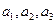 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | 3 | 2 | 10 |
第二行 | 6 | 4 | 14 |
第三行 | 9 | 8 | 18 |
(Ⅰ) 求数列
求数列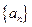 的通项公式;
的通项公式;
(Ⅱ)若数列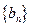 满足:
满足: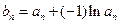 ,求数列
,求数列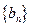 的前
的前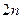 项和
项和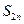 .
.
【解析】(Ⅰ)由题意知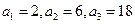 ,因为
,因为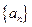 是等比数列,所以公比为3,所以数列
是等比数列,所以公比为3,所以数列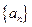 的通项公式
的通项公式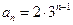 .
.
(Ⅱ)因为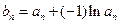 =
=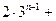
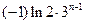 , 所以
, 所以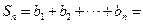
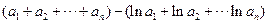 =
=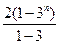 -
-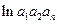 =
=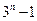 -
-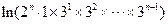 =
=
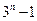 -
-
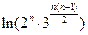 ,所以
,所以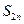 =
=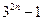 -
-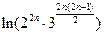 =
=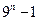 -
-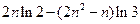 .
.
21.(本小题满分 12分)
12分)
某 企
企 业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为
业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为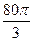 立方米,且
立方米,且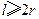 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为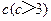 .设该容器的建造费用为
.设该容器的建造费用为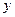 千元.
千元.

(Ⅰ)写出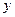 关于
关于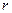 的函数表达式,并求该函
的函数表达式,并求该函 数的定义域;
数的定义域;
(Ⅱ)求该容器的建造费用最小时的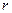 .
.
【解析】(Ⅰ)因为容器的体积为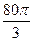 立方米,所以
立方米,所以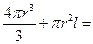
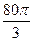 ,解得
,解得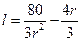 ,所以圆柱的侧面积为
,所以圆柱的侧面积为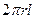 =
=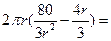
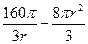 ,两端两个半球的表面积之和为
,两端两个半球的表面积之和为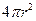 ,所以
,所以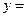
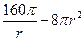 +
+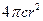 ,定义域为(0,
,定义域为(0,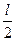 ).
).
(Ⅱ)因为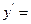
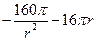 +
+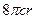 =
=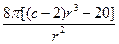 ,所以令
,所以令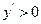 得:
得: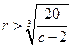 ; 令
; 令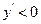 得:
得: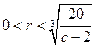 ,所以
,所以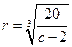 米时, 该容器的建造费用最小.
米时, 该容器的建造费用最小.
22.(本小题满分14分)
已知动直线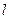 与椭圆C:
与椭圆C: 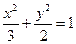 交于P
交于P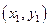 、Q
、Q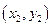 两不同点,且△OPQ的面积
两不同点,且△OPQ的面积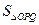 =
=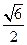 ,其中O为坐标原点.
,其中O为坐标原点.
(Ⅰ)证明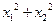 和
和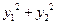 均为定值;
均为定值;
(Ⅱ)设线段PQ的中点为M,求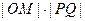 的最大值;
的最大值;
(Ⅲ)椭圆C上是否存在点D,E,G,使得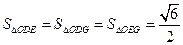 ?若存在,判断△DEG的形状;若不存在,请说明理由.
?若存在,判断△DEG的形状;若不存在,请说明理由.
【解析】(参考标准答案)












